Closure space

Let be a set and the set of subsets of . A function is a closure operation if for all :

K1) ;

K2) ;

K3) ;

K4) ;

K5) . These are the Kuratowski closure axioms, and a function satisfying these axioms is called a Kuratowski closure operator (or Kuratowski closure operation).

A pair 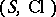is a closure space if and only if satisfies:

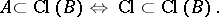This condition is equivalent to K1)–K3). A closure space that satisfies K5) is a Fréchet -space. A Fréchet -space that satisfies K4) is a topological space.

A Čech closure operator is a mapping 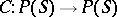such that

C1) ;

C2) ( K1)) ;

C3) . A set endowed with a Čech closure operator is called a pre-topological space.

References

[a1]	N.M. Martin, S. Pollard, "Closure spaces and logic" , Kluwer Acad. Publ. (1996)
[a2]	J.L. Kelley, "General topology" , v. Nostrand–Reinhold (1955)
[a3]	D. Dikranjan, W. Tholin, "Categorical structures of closure operators" , Kluwer Acad. Publ. (1996)