Surface integral
An integral over a surface. Let a surface 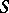 in the three-dimensional Euclidean space
in the three-dimensional Euclidean space 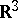 , possibly with self-intersections, be specified by the vector representation
, possibly with self-intersections, be specified by the vector representation
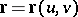 | (1) |
in Cartesian coordinates 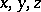 , where
, where  is a continuously-differentiable vector function defined on the closure
is a continuously-differentiable vector function defined on the closure 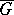 of a two-dimensional Jordan-measurable domain
of a two-dimensional Jordan-measurable domain 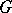 lying in the plane with Cartesian coordinates
lying in the plane with Cartesian coordinates  and
and  . Let
. Let
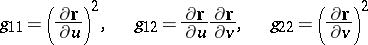 |
be the coefficients of the first fundamental form of 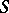 . If
. If 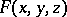 is a function defined on
is a function defined on 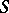 , i.e. a function
, i.e. a function 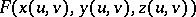 , then the following defines the surface integral of the first kind (or the integral over the surface area):
, then the following defines the surface integral of the first kind (or the integral over the surface area):
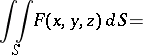 | (2) |
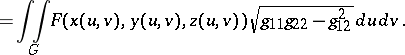 |
This definition is independent of the representation of the surface. A surface integral of the first kind is the limit of corresponding Riemann sums, which may be described in terms related to the surface. For example, if 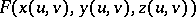 is a Riemann-integrable function, if
is a Riemann-integrable function, if 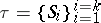 is a decomposition of
is a decomposition of  into parts
into parts 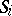 that are images under the mapping (1) of sets
that are images under the mapping (1) of sets 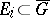 forming a decomposition
forming a decomposition 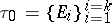 of
of 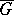 (see Multiple integral) and if
(see Multiple integral) and if
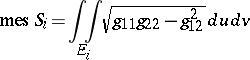 |
is the area of 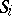 , then
, then
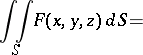 |
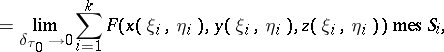 |
where 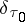 is the fineness (mesh) of
is the fineness (mesh) of 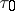 and
and 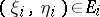 . If
. If 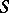 is explicitly specified in the form
is explicitly specified in the form  ,
, 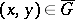 , (2) becomes
, (2) becomes
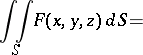 |
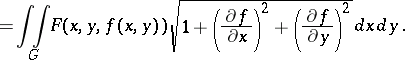 |
If there are no singular points on a surface 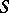 with vector representation (1), i.e. if
with vector representation (1), i.e. if 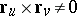 , then
, then 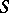 can be oriented by selecting a continuous unit normal
can be oriented by selecting a continuous unit normal 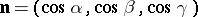 on it, for example
on it, for example
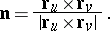 |
For an oriented surface 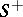 one defines the surface integrals of the second kind by
one defines the surface integrals of the second kind by
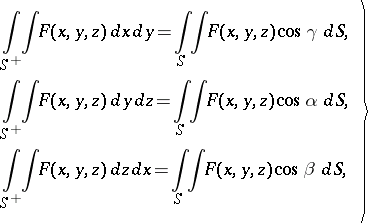 | (3) |
where surface integrals of the first kind appear on the right-hand side. If 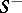 is the surface
is the surface 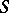 with orientation opposite to that of
with orientation opposite to that of 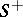 , then
, then
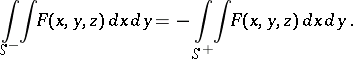 |
Similar equations apply to the other surface integrals of the second kind in (3). Surface integrals of the second kind resemble those of the first kind in being the limits of Riemann sums, which can be described in terms of the surface.
If
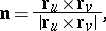 |
then
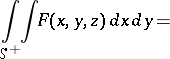 |
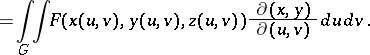 |
Similar formulas apply to the other surface integrals of the second kind in (3).
In particular, for the case of a surface 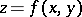 ,
, 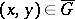 ,
,
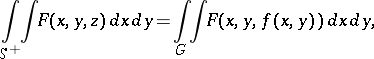 |
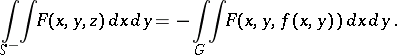 |
The first of these integrals is called an integral over the "upper" side of  and the second over the "lower" side. This terminology is used because the vector
and the second over the "lower" side. This terminology is used because the vector
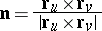 |
forms an acute angle with the  -axis in the case of an explicit specification of
-axis in the case of an explicit specification of 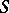 , i.e. when
, i.e. when  ,
,  and
and 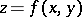 , i.e. it is directed "upwards" , while in the second case it forms an obtuse angle and is thus directed "downwards" .
, i.e. it is directed "upwards" , while in the second case it forms an obtuse angle and is thus directed "downwards" .
If a smooth surface 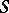 is the boundary of a bounded domain and
is the boundary of a bounded domain and 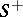 denotes its orientation by means of the outward normal, hence
denotes its orientation by means of the outward normal, hence  is determined by the inward normal, with respect to the domain, then the surface integrals of the second kind over the oriented surface
is determined by the inward normal, with respect to the domain, then the surface integrals of the second kind over the oriented surface 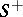 are called surface integrals with respect to the outside of the surface, while those over
are called surface integrals with respect to the outside of the surface, while those over 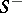 are called surface integrals with respect to the inside.
are called surface integrals with respect to the inside.
The surface integrals for a piecewise-smooth surface that can be divided into a finite number of parts each of which has a vector representation (1) are defined as the sums of the surface integrals over the corresponding parts. Thus, surface integrals defined with respect to piecewise-smooth surfaces are not dependent on the method of dividing the surfaces into those parts.
The Ostrogradski formula establishes a relationship between a triple integral over a three-dimensional bounded domain and the surface integrals over its boundary, while the Stokes formula gives a relationship between a surface integral and the curvilinear integral over the contour representing the boundary.
The surface integral 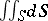 is equal to the area of
is equal to the area of 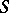 . If a mass with density
. If a mass with density 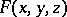 is distributed on
is distributed on 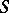 , then the surface integral
, then the surface integral 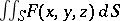 is equal to the entire mass. If
is equal to the entire mass. If 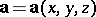 is a vector function specified on a surface
is a vector function specified on a surface 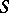 that is oriented by means of the unit normal
that is oriented by means of the unit normal 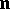 , then the surface integral
, then the surface integral
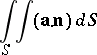 |
is called the flux of the vector field  through
through 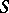 . Clearly, this is independent of the choice of a coordinate system in
. Clearly, this is independent of the choice of a coordinate system in  . One also uses surface integrals to describe a double-layer potential or a simple-layer potential.
. One also uses surface integrals to describe a double-layer potential or a simple-layer potential.
If the surface  is a differentiable
is a differentiable  -manifold, if the continuously-differentiable non-negative functions
-manifold, if the continuously-differentiable non-negative functions 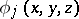 ,
, 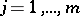 , form a partition of unity on
, form a partition of unity on 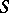 , i.e. the support of each function is contained in some chart of
, i.e. the support of each function is contained in some chart of 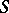 and
and 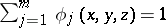 for each point
for each point 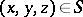 , and if
, and if 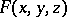 is a function defined on
is a function defined on 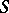 , then by definition
, then by definition
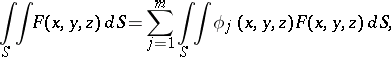 | (4) |
where each integral on the right-hand side is understood in the sense of (2). If 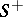 is an oriented two-dimensional manifold, then
is an oriented two-dimensional manifold, then
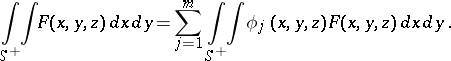 | (5) |
The other types of surface integrals of the second kind in (3) are defined similarly. The definitions (4) and (5) are independent of the choice of a partition of unity in 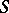 .
.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "Mathematical analysis" , Moscow (1973) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [4] | B.A. Dubrovin, A.T. Fomenko, S.P. Novikov, "Modern geometry" , Springer (1987) (Translated from Russian) |
| [5] | A.S. Mishchenko, A.T. Fomenko, "A course of differential geometry and topology" , MIR (1988) (Translated from Russian) |
Comments
Ostrogradski's formula is usually called Gauss' formula in the West. The phrase divergence theorem is also used.
In vector notation one can write
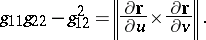 |
The distinction between surface integrals of the first and the second kind is not common in Western literature.
Integrals over differentiable  -dimensional manifolds can be conveniently defined using
-dimensional manifolds can be conveniently defined using  -forms. See, e.g., [a4] and Integration on manifolds.
-forms. See, e.g., [a4] and Integration on manifolds.
References
| [a1] | G.E. Shilov, "Mathematical analysis" , 1–2 , M.I.T. (1974) (Translated from Russian) |
| [a2] | T.M. Apostol, "Calculus" , 2 , Waltham (1969) |
| [a3] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) |
| [a4] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a5] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5 |
| [a6] | J.J. Stoker, "Differential geometry" , Wiley (Interscience) (1969) |
| [a7] | D.J. Struik, "Lectures on classical differential geometry" , Addison-Wesley (1961) |
| [a8] | R.C. Buck, "Advanced calculus" , McGraw-Hill (1965) |
| [a9] | W. Fleming, "Functions of several variables" , Springer (1977) |
| [a10] | J. Marsden, A. Weinstein, "Calculus" , 3 , Springer (1988) |
Surface integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Surface_integral&oldid=39866