Clifford parallel
A straight line in an elliptic space that stays at a constant distance from a given (base) straight line. Through each point lying outside a given line and outside its polar line there pass two Clifford parallels to the given line. The surface formed by rotating a Clifford parallel about its base line is called a Clifford surface. A Clifford surface has constant zero Gaussian curvature.
W. Clifford (1873) was the first to show the existence of Clifford surfaces.
References
| [1] | S.A. Bogomolov, "An introduction to Riemann's non-Euclidean geometry" , Leningrad-Moscow (1934) (In Russian) |
| [2] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
Comments
Let 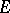 be
be 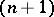 -dimensional Euclidean space, and
-dimensional Euclidean space, and  its associated projective space of all straight lines through the origin. For
its associated projective space of all straight lines through the origin. For 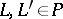 let
let  be the angle between the lines
be the angle between the lines  and
and  in
in  . Then
. Then  with this metric is called the elliptic space associated with
with this metric is called the elliptic space associated with  . The topology induced by this metric is the usual one, i.e. the quotient topology of
. The topology induced by this metric is the usual one, i.e. the quotient topology of 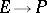 . The article above deals with the case
. The article above deals with the case 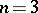 .
.
The (absolute) polar line to the line 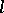 through two points
through two points 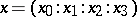 and
and 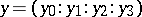 of
of  is the line of all points
is the line of all points 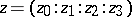 such that
such that  , where
, where  denotes the usual inner product.
denotes the usual inner product.
The notion of Clifford parallelism is also considered on the  -fold covering
-fold covering 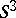 of
of  , [a2].
, [a2].
References
| [a1] | F. Klein, "Vorlesungen über nichteuklidische Geometrie" , Springer (1928) |
| [a2] | M. Berger, "Geometry" , II , Springer (1987) pp. 84 |
Clifford parallel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Clifford_parallel&oldid=39863