Borel set of ambiguous class
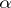
A Borel subset of a metric, or (more general) of a perfectly-normal topological, space that is at the same time a set of additive class 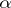 and of multiplicative class
and of multiplicative class 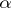 , i.e. belongs to the classes
, i.e. belongs to the classes  and
and  at the same time. Borel sets of ambiguous class 0 are the closed and open sets. Borel sets of ambiguous class 1 are sets of types
at the same time. Borel sets of ambiguous class 0 are the closed and open sets. Borel sets of ambiguous class 1 are sets of types 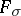 and
and 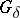 at the same time. Any Borel set of class
at the same time. Any Borel set of class 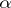 is a Borel set of ambiguous class
is a Borel set of ambiguous class 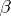 for any
for any 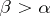 . The Borel sets of ambiguous class
. The Borel sets of ambiguous class 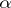 form a field of sets.
form a field of sets.
References
| [1] | K. Kuratowski, "Topology" , 1 , Acad. Press (1966) (Translated from French) |
| [2] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
Comments
The notations 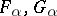 are still current in topology. Outside topology one more often uses the notation
are still current in topology. Outside topology one more often uses the notation  ,
, 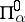 , respectively. For
, respectively. For 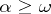 one has
one has 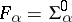 ,
, 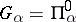 ; but
; but 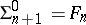 and
and 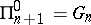 for
for 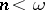 . The notation for the ambiguous classes is
. The notation for the ambiguous classes is 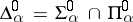 . See also [a1].
. See also [a1].
References
| [a1] | Y.N. Moschovakis, "Descriptive set theory" , North-Holland (1980) |
Borel set of ambiguous class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_set_of_ambiguous_class&oldid=39789