Geodesic mapping
projective mapping
A mapping 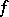 that transforms the geodesic lines of a space
that transforms the geodesic lines of a space 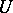 into the geodesic lines of a space
into the geodesic lines of a space 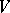 . A geodesic mapping
. A geodesic mapping  , where
, where 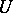 and
and  are spaces in which geodesics are defined, is a local homeomorphism (diffeomorphism if
are spaces in which geodesics are defined, is a local homeomorphism (diffeomorphism if 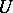 and
and 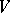 are smooth manifolds).
are smooth manifolds).
A space that locally permits a geodesic mapping into a Euclidean space is called projectively flat. Geodesic mappings of one Riemannian space into another exist in exceptional cases. Among the Riemannian spaces only those of constant curvature are projectively flat [1]. The description of all Riemannian projectively-flat metric spaces constitutes Hilbert's fourth problem [2].
In the theory of spaces with an affine connection one does not speak of geodesic mappings but rather of geodesic transformations of a connection, which means a transition to another connection on the same manifold with preservation of the geodesics. The transition from a connection 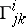 to a connection
to a connection 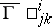 is a geodesic mapping under the condition
is a geodesic mapping under the condition 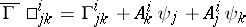 , where
, where 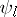 is a covector field. A space with an affine connection is projectively flat if and only if the projective curvature tensor vanishes.
is a covector field. A space with an affine connection is projectively flat if and only if the projective curvature tensor vanishes.
References
| [1] | J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) (Translated from German) |
| [2] | A.V. Pogorelov, "Hilbert's fourth problem" , Winston & Wiley (1979) (In Russian) |
Geodesic mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geodesic_mapping&oldid=39679