Kernel of a loop

The set of elements of the loop that are simultaneously left-, right- and middle-associative (or, equivalently, the intersection of the left, right and middle kernels of the loop). An element of a loop is called left-associative if for any 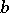, in the loop. The set of left-associative elements is called the left kernel of the loop. Right- and middle-associative elements and the corresponding kernels are defined similarly. Left and right kernels can also be defined for quasi-groups, but only loops have a non-empty middle kernel. All the kernels of a loop are subgroups of it. All three kernels of a 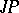-loop coincide, and for Moufang loops (cf. Moufang loop) they form, in addition, a normal subloop (see Loop).