Decision function

decision procedure, statistical decision rule

A rule according to which statistical decisions are made on the basis of observations obtained.

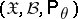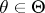Let be a random variable that takes values in a sampling space , , and let 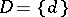be the set of all possible decisions 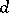that can be taken relative to the parameter 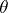with respect to a realization of 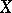. According to the accepted terminology in mathematical statistics and the theory of games, any 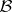-measurable transformation 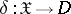of the space of realizations 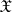of 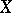into the set of possible decisions 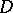is called a decision function. For example, in the statistical estimation of the parameter 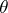any point estimator 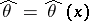is a decision function. A basic problem in statistics in obtaining statistical conclusions is the choice of a decision function 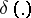that minimizes the risk

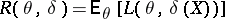relative to the loss function 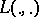used.

The concept of a decision function is a basic concept in the theory of statistical decision functions as developed by A. Wald.

References

[1]	N.N. Chentsov, "Statistical decision laws and optimal inference" , Amer. Math. Soc. (1982) (Translated from Russian)
[2]	A. Wald, "Statistical decision functions" , Wiley (1950)

Comments

Cf. also Statistical decision theory.

References

[a1]	J.O. Berger, "Statistical decision theory. Foundations, concepts and models" , Springer (1980)