Triad
Quadruples  , where
, where 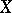 is a topological space and
is a topological space and 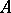 and
and 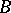 are subspaces of it such that
are subspaces of it such that 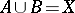 and
and 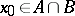 . The homotopy groups of triads,
. The homotopy groups of triads, 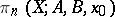 ,
, 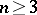 (for
(for  , it is just a set), have been introduced and are used in the proof of homotopy excision theorems. There is also an exact Mayer–Vietoris sequence connecting the homology groups of the spaces
, it is just a set), have been introduced and are used in the proof of homotopy excision theorems. There is also an exact Mayer–Vietoris sequence connecting the homology groups of the spaces 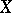 ,
, 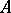 ,
, 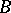 ,
, 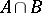 (cf. Homology group).
(cf. Homology group).
Comments
For a triple 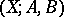 consisting of a space
consisting of a space  and two subspaces
and two subspaces 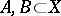 , one defines the path space
, one defines the path space 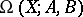 as the space of all paths in
as the space of all paths in  starting in
starting in  and ending in
and ending in  ,
,
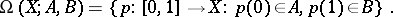 |
If there is a distinguished point  in
in 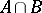 , the constant path at
, the constant path at  is taken as a distinguished point of
is taken as a distinguished point of 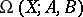 (and is also denoted by
(and is also denoted by  ).
).
The relative homotopy groups (cf. Homotopy group)  ,
,  , can also be defined as
, can also be defined as 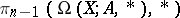 . Now let
. Now let 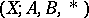 be a triad. The homotopy groups of a triad are defined as the relative homotopy groups
be a triad. The homotopy groups of a triad are defined as the relative homotopy groups
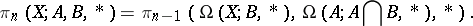 |
Using the long homotopy sequence of the triplet 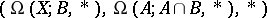 there results the (first) homotopy sequence of a triad
there results the (first) homotopy sequence of a triad
 |
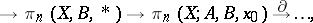 |
so that the triad homotopy groups measure the extend to which the homotopy excision homomorphisms
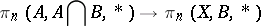 |
fail to be isomorphisms. The triad homotopy groups can also be defined as
 |
References
| [a1] | S.-T. Hu, "Homotopy theory" , Acad. Press (1955) pp. Chapt. V, §10 |
| [a2] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. 88 |
| [a3] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. §6.17 |
Triad. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Triad&oldid=38847