Strong integral

An integral of Lebesgue type either of a function with values in a linear topological space with respect to a scalar measure, or of a scalar function with respect to a measure with values in a vector space. Here the limit processes by which the integral is defined are taken in the sense of the strong topology. Examples of strong integrals are:

1) the Bochner integral of a vector-valued function;

2) the Daniell integral, if the values of the integrand belong to a 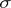-complete vector lattice;

3) the integral 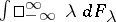, giving the spectral decomposition of a self-adjoint operator acting on a Hilbert space (cf. Spectral decomposition of a linear operator).

For the strong integral of scalar functions with respect to a vector measure, the values of the measure, in many cases, are assumed to belong to a semi-ordered vector space (cf. Semi-ordered space).

References

[1a]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958)
[1b]	N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963)
[2]	T.H. Hildebrandt, "Integration in abstract spaces" Bull. Amer. Math. Soc. , 59 (1953) pp. 111–139

Comments

See also Vector measure; Strong topology.

References

[a1]	J. Diestel, J.J. Uhl jr., "Vector measures" , Math. Surveys , 15 , Amer. Math. Soc. (1977)