Spectral measure
From Encyclopedia of Mathematics
A unitary homomorphism from some Boolean algebra of sets into the Boolean algebra of projection operators on a Banach space. Every operator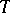 
on a Banach space 
defines a spectral measure on the set of open-and-closed subsets of its spectrum 
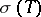by the formula
 |
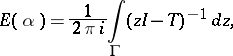where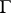 
is a Jordan curve separating 
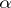from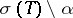 
. Here, 
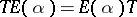and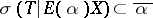 
. The construction of spectral measures satisfying these conditions on wider classes of Boolean algebras of sets is one of the basic problems in the spectral theory of linear operators.
References
| [1a] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral operators" , 3 , Interscience (1971) |
| [1b] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) |
How to Cite This Entry:
Spectral measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_measure&oldid=38617
Spectral measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_measure&oldid=38617
This article was adapted from an original article by V.S. Shul'man (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article