Normal extension
of a field 
An algebraic field extension (cf. Extension of a field)  of
of  satisfying one of the following equivalent conditions:
satisfying one of the following equivalent conditions:
1) any imbedding of  in the algebraic closure
in the algebraic closure  of
of  comes from an automorphism of
comes from an automorphism of  ;
;
2)  is the splitting field of some family of polynomials with coefficients in
is the splitting field of some family of polynomials with coefficients in  (cf. Splitting field of a polynomial);
(cf. Splitting field of a polynomial);
3) any polynomial 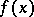 with coefficients in
with coefficients in  , irreducible over
, irreducible over 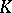 and having a root in
and having a root in 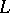 , splits in
, splits in 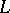 into linear factors.
into linear factors.
For every algebraic extension 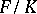 there is a maximal intermediate subfield
there is a maximal intermediate subfield 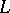 that is normal over
that is normal over 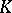 ; this is the field
; this is the field 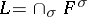 , where
, where 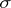 ranges over all imbeddings of
ranges over all imbeddings of  in
in 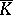 . There is also a unique minimal normal extension of
. There is also a unique minimal normal extension of  containing
containing  . This is the composite of all fields
. This is the composite of all fields 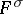 . It is called the normal closure of the field
. It is called the normal closure of the field 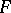 relative to
relative to  . If
. If  and
and 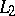 are normal extensions of
are normal extensions of 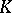 , then so are the intersection
, then so are the intersection  and the composite
and the composite 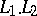 . However, when
. However, when 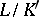 and
and 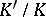 are normal extensions,
are normal extensions,  need not be normal.
need not be normal.
For fields of characteristic zero every normal extension is a Galois extension. In general, a normal extension is a Galois extension if and only if it is separable (cf. Separable extension).
References
| [1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1984) |
| [3] | M.M. Postnikov, "Fundamentals of Galois theory" , Noordhoff (1962) (Translated from Russian) |
Normal extension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_extension&oldid=38571