Frobenius algebra
A finite-dimensional algebra 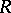 over a field
over a field 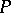 such that the left
such that the left 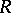 -modules
-modules 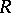 and
and 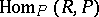 are isomorphic. In the language of representations this means that the left and right regular representations are equivalent. Every group algebra of a finite group over a field is a Frobenius algebra. Every Frobenius algebra is a quasi-Frobenius ring. The converse is not true. The following properties of a finite-dimensional
are isomorphic. In the language of representations this means that the left and right regular representations are equivalent. Every group algebra of a finite group over a field is a Frobenius algebra. Every Frobenius algebra is a quasi-Frobenius ring. The converse is not true. The following properties of a finite-dimensional 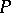 -algebra
-algebra 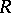 are equivalent:
are equivalent:
1) 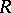 is a Frobenius algebra;
is a Frobenius algebra;
2) there is a non-degenerate bilinear form 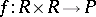 such that
such that 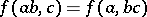 for all
for all 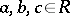 ;
;
3) if 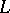 is a left and
is a left and 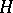 is a right ideal of
is a right ideal of 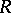 , then (see Annihilator)
, then (see Annihilator)
 |
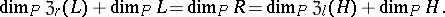 |
Frobenius algebras essentially first appeared in the papers of G. Frobenius [3].
References
| [1] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
| [2] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1973–1976) |
| [3] | G. Frobenius, "Theorie der hyperkomplexen Grössen" Sitzungsber. Königl. Preuss. Akad. Wiss. : 24 (1903) pp. 504–537; 634–645 |
Comments
A criterion for an algebra 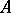 to be Frobenius is that there is a linear form
to be Frobenius is that there is a linear form 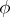 on
on 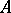 such that if
such that if  for all
for all 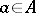 then
then 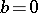 . If, moreover,
. If, moreover, 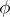 satisfies
satisfies 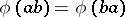 for all
for all 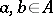 , then
, then 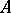 is called a symmetric algebra.
is called a symmetric algebra.
Examples of symmetric algebras are semi-simple algebras and group algebras.
Frobenius algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frobenius_algebra&oldid=37655