Krawtchouk polynomials

Polynomials orthogonal on the finite system of integer points whose distribution function is a step function with discontinuities:

where is the binomial coefficient (cf. Binomial coefficients), and . The Krawtchouk polynomials are given by the formulas

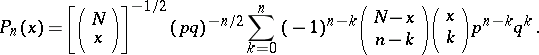The concept is due to M.F. Krawtchouk [1].

References

[1]	M.F. Krawtchouk, "Sur une généralisation des polynômes d'Hermite" C.R. Acad. Sci. Paris , 189 (1929) pp. 620–622
[2]	G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)

Comments

Krawtchouk polynomials can be written as hypergeometric functions (cf. Hypergeometric function) of type . The unitarity relations for the matrix elements of the irreducible unitary representations of the group can be rewritten as the orthogonality relations for the Krawtchouk polynomials, cf. [a2], [a3]. These polynomials have also an interpretation as spherical functions on wreath products (cf. Wreath product) of symmetric groups, cf. [a4], where -Krawtchouk polynomials are also treated. Coding theorists rather (but equivalently) relate them to Hamming schemes, where Krawtchouk polynomials are used for dealing with problems about perfect codes, cf. [a1].

References

[a1]	J.H. van Lint, "Introduction to coding theory" , Springer (1982)
[a2]	T.H. Koornwinder, "Krawtchouk polynomials, a unification of two different group theoretic interpretations" SIAM J. Math. Anal. , 13 (1982) pp. 1011–1023
[a3]	V.B. Uvarov, "Special functions of mathematical physics" , Birkhäuser (1988) (Translated from Russian)
[a4]	D. Stanton, "Orthogonal polynomials and Chevalley groups" R.A. Askey (ed.) T.H. Koornwinder (ed.) W. Schempp (ed.) , Special functions: group theoretical aspects and applications , Reidel (1984) pp. 87–128