Distributive lattice

A lattice in which the equation

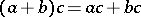holds. This equation is equivalent to both

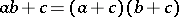and

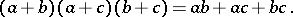Distributive lattices are characterized by the fact that all their convex sublattices can occur as congruence classes. Any distributive lattice is isomorphic to a lattice of (not necessarily all) subsets of some set. An important special case of such lattices are Boolean algebras (cf. Boolean algebra). For any finite set in a distributive lattice the following equalities are valid:

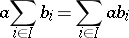and

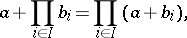as well as

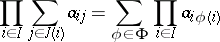and

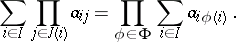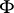Here the are finite sets and is the set of all single-valued functions 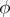from into 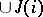such for each 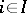. In a complete lattice the above equations also have a meaning if the sets and 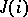are infinite. However, they do not follow from the distributive law. Distributive complete lattices (cf. Complete lattice) which satisfy the two last-mentioned identities for all sets and 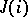are called completely distributive.

References

[1]	G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973)
[2]	L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian)
[3]	G. Grätzer, "General lattice theory" , Birkhäuser (1978) (Original: Lattice theory. First concepts and distributive lattices. Freeman, 1978)

Comments

The distributive property of lattices may be characterized by the presence of enough prime filters: A lattice is distributive if and only if its prime filters separate its points, or, equivalently, if, give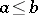n in 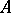, there exists a lattice homomorphism 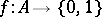with 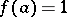and , [a1]. In the study of distributive lattices, their topological representation plays an important role; this was first established by M.H. Stone [a2], and reformulated in more convenient terms by H.A. Priestley [a3] — both versions generalize the Stone duality for Boolean algebras (cf. also Stone space). To describe Priestley's version, let 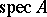denote the set of prime filters of a distributive lattice , partially ordered by inclusion and topologized by declaring the sets

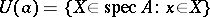and their complements to be subbasic open sets. Then the assignment is a lattice-isomorphism from 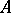to the set of clopen (i.e. closed and open) subsets of 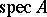which are upward closed in the partial order. Moreover, the partially ordered spaces which occur as for some are precisely the compact spaces in which, given 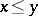, there exists a clopen upward-closed set containing but not — such spaces are sometimes called Priestley spaces. Note that a Priestley space is discretely ordered if and only if every prime filter of 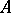is maximal, if and only if is a Boolean algebra. Other important classes of distributive lattices can similarly be characterized by order-theoretic and/or topological properties of their Priestley spaces (see [a4]).

In addition to the general references [1]–[3] above, [a5] may also be recommended as a general account of distributive lattice theory.

For completely distributive lattices see Completely distributive lattice.

References

[a1]	G. Birkhoff, "On the combination of subalgebras" Proc. Cambr. Philos. Soc. , 29 (1933) pp. 441–464
[a2]	M.H. Stone, "Topological representation of distributive lattices and Brouwerian logics" Časopis Pešt. Mat. Fys. , 67 (1937) pp. 1–25
[a3]	H.A. Priestley, "Ordered topological spaces and the representation of distributive lattices" Proc. Lond. Math. Soc. (3) , 24 (1972) pp. 507–530
[a4]	H.A. Priestley, "Ordered sets and duality for distributive lattices" , Orders: Description and Roles , Ann. Discrete Math. , 23 , North-Holland (1984) pp. 39–60
[a5]	R. Balbes, P. Dwinger, "Distributive lattices" , Univ. Missouri Press (1974)