Affine coordinate frame
A set of  linearly-independent vectors
linearly-independent vectors 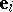 (
(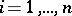 ) of
) of  -dimensional affine space
-dimensional affine space 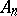 , and a point
, and a point  . The point
. The point 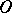 is called the initial point, while the vectors
is called the initial point, while the vectors 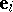 are the scale vectors. Any point
are the scale vectors. Any point 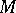 is defined with respect to the affine coordinate frame by
is defined with respect to the affine coordinate frame by  numbers — coordinates
numbers — coordinates 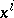 , occurring in the decomposition of the position vector
, occurring in the decomposition of the position vector 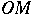 by the scale vectors:
by the scale vectors: 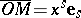 (summation convention). The specification of two affine coordinate frames defines a unique affine transformation of the space
(summation convention). The specification of two affine coordinate frames defines a unique affine transformation of the space 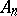 which converts the first frame into the second (see also Affine coordinate system).
which converts the first frame into the second (see also Affine coordinate system).
Comments
An equivalent, and more usual, definition is as follows. An affine coordinate frame in affine  -space is a set of
-space is a set of 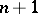 points
points  which are linearly independent in the affine sense, i.e. the vectors
which are linearly independent in the affine sense, i.e. the vectors 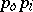 ,
, 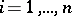 , are linearly independent in the corresponding vector space. Independence of the vectors
, are linearly independent in the corresponding vector space. Independence of the vectors  in the definition should be understood as independence in a corresponding vector space.
in the definition should be understood as independence in a corresponding vector space.
References
| [1] | E. Snapper, R.J. Troyer, "Metric affine geometry" , Acad. Press (1971) |
Affine coordinate frame. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_coordinate_frame&oldid=37609