Dirichlet process
The Dirichlet process provides one means of placing a probability distribution on the space of distribution functions, as is done in Bayesian statistical analysis (cf. also Bayesian approach). The support of the Dirichlet process is large: For each distribution function there is a set of distributions nearby that receives positive probability. This contrasts with a typical probability distribution on the space of distribution functions where, for example, one might place a probability distribution on the mean and variance of a normal distribution. The support in this example would be contained in the collection of normal distributions. The large support of the Dirichlet process accounts for its use in non-parametric Bayesian analysis. General references are [a4], [a5].
The Dirichlet process is indexed by its parameter, a non-null, finite measure  . Formally, consider a space
. Formally, consider a space 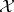 with a collection of Borel sets
with a collection of Borel sets 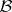 on
on 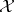 . The random probability distribution
. The random probability distribution 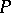 has a Dirichlet process prior distribution with parameter
has a Dirichlet process prior distribution with parameter 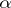 , denoted by
, denoted by 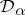 , if for every measurable partition
, if for every measurable partition  of
of 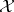 the random vector
the random vector 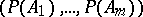 has the Dirichlet distribution with parameter vector
has the Dirichlet distribution with parameter vector 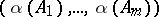 .
.
When a prior distribution is put on  , then for every measurable subset
, then for every measurable subset  of
of  , the quantity
, the quantity 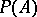 is a random variable. Then
is a random variable. Then 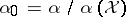 is a probability measure on
is a probability measure on 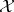 . From the definition one sees that if
. From the definition one sees that if 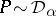 , then
, then 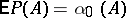 .
.
An alternative representation of the Dirichlet process is given in [a6]: Let 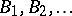 be independent and identically distributed
be independent and identically distributed 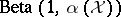 random variables, and let
random variables, and let 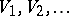 be a sequence of independent and identically distributed random variables with distribution
be a sequence of independent and identically distributed random variables with distribution 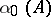 , and independent of the random variables
, and independent of the random variables 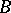 . Define
. Define 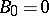 , and
, and 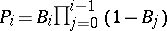 . The random distribution
. The random distribution 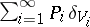 has the distribution
has the distribution 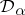 . Here,
. Here, 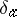 represents the point mass at
represents the point mass at  . This representation makes clear the fact that the Dirichlet process assigns probability one to the set of discrete distributions, and emphasizes the role of the mass of the measure
. This representation makes clear the fact that the Dirichlet process assigns probability one to the set of discrete distributions, and emphasizes the role of the mass of the measure 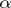 . For example, as
. For example, as 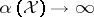 ,
, 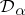 converges to the point mass at
converges to the point mass at 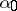 (in the weak topology induced by
(in the weak topology induced by 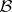 ); and as
); and as 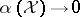 ,
, 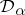 converges to the random distribution which is degenerate at a point
converges to the random distribution which is degenerate at a point 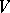 , whose location has distribution
, whose location has distribution 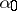 .
.
The Dirichlet process is conjugate, in that if 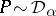 , and data points
, and data points 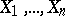 independent and identically drawn from
independent and identically drawn from  are observed, then the conditional distribution of
are observed, then the conditional distribution of 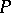 given
given 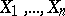 is
is 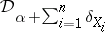 . This conjugation property is an extension of the conjugacy of the Dirichlet distribution for multinomial data. It ensures the existence of analytical results with a simple form for many problems. The combination of simplicity and usefulness has given the Dirichlet process its reputation as the standard non-parametric model for a probability distribution on the space of distribution functions.
. This conjugation property is an extension of the conjugacy of the Dirichlet distribution for multinomial data. It ensures the existence of analytical results with a simple form for many problems. The combination of simplicity and usefulness has given the Dirichlet process its reputation as the standard non-parametric model for a probability distribution on the space of distribution functions.
An important extension of the class of Dirichlet processes is the class of mixtures of Dirichlet processes. A mixture of Dirichlet processes is a Dirichlet process in which the parameter measure is itself random. In applications, the parameter measure ranges over a finite-dimensional parametric family. Formally, one considers a parametric family of probability distributions 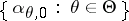 . Suppose that for every
. Suppose that for every 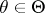 ,
, 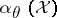 is a positive constant, and let
is a positive constant, and let 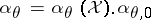 . If
. If  is a probability distribution on
is a probability distribution on 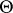 , and if, first,
, and if, first, 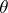 is chosen from
is chosen from  , and then
, and then 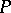 is chosen from
is chosen from 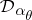 , one says that the prior on
, one says that the prior on 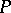 is a mixture of Dirichlet processes (with parameter
is a mixture of Dirichlet processes (with parameter 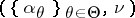 ). A reference for this is [a1]. Often,
). A reference for this is [a1]. Often, 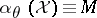 , i.e., the constants
, i.e., the constants 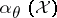 do not depend on
do not depend on  . In this case, large values of
. In this case, large values of 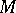 indicate that the prior on
indicate that the prior on 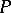 is "concentrated around the parametric family aq,0qQ" . More precisely, as
is "concentrated around the parametric family aq,0qQ" . More precisely, as 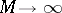 , the distribution of
, the distribution of 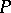 converges to
converges to 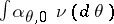 , the standard Bayesian model for the parametric family
, the standard Bayesian model for the parametric family 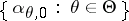 in which
in which 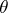 has prior
has prior  .
.
The Dirichlet process has been used in many applications. A particularly interesting one is the Bayesian hierarchical model, which is the Bayesian version of the random effects model. A typical example is as follows. Suppose one is studying the success of a certain type of operation for patients from different hospitals. Suppose one has 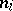 patients in hospital
patients in hospital 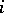 ,
, 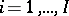 . One might model the number of failures
. One might model the number of failures 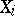 in hospital
in hospital 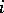 as a binomial distribution, with success probability depending on the hospital. And one might wish to view the
as a binomial distribution, with success probability depending on the hospital. And one might wish to view the 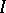 binomial parameters as being independent and identically distributed drawn from a common distribution. The typical hierarchical model then is written as
binomial parameters as being independent and identically distributed drawn from a common distribution. The typical hierarchical model then is written as
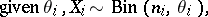 | (a1) |
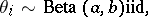 |
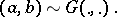 |
Here, the 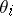 are unobserved, or latent, variables. If the distribution
are unobserved, or latent, variables. If the distribution 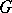 was degenerate, then the
was degenerate, then the 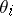 would be independent, so that data from one hospital would not give any information on the success rate from any other hospital. On the other hand, when
would be independent, so that data from one hospital would not give any information on the success rate from any other hospital. On the other hand, when 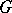 is not degenerate, then data coming from the other hospitals provide some information on the success rate of hospital
is not degenerate, then data coming from the other hospitals provide some information on the success rate of hospital 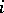 .
.
Consider now the problem of prediction of the number of successes for a new hospital, indexed 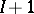 . A disadvantage of the model (a1) is that if the
. A disadvantage of the model (a1) is that if the 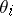 are independent and identically drawn from a distribution which is not a Beta, then even as
are independent and identically drawn from a distribution which is not a Beta, then even as 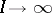 , the predictive distribution of
, the predictive distribution of 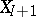 based on the (incorrect) model (a1) need not converge to the actual predictive distribution of
based on the (incorrect) model (a1) need not converge to the actual predictive distribution of 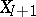 . An alternative model, using a mixture of Dirichlet processes prior, would be written as
. An alternative model, using a mixture of Dirichlet processes prior, would be written as
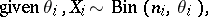 | (a2) |
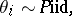 |
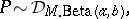 |
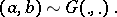 |
The model (a2) does not have the defect suffered by (a1), because the support of the distribution on 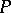 is the set of all distributions concentrated in the interval
is the set of all distributions concentrated in the interval 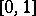 .
.
It is not possible to obtain closed-form expressions for the posterior distributions in (a2). Computational schemes to obtain these have been developed by M. Escobar and M. West [a3] and C.A. Bush and S.N. MacEachern [a2].
The parameter 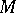 plays an interesting role. When
plays an interesting role. When 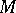 is small, then, with high probability, the
is small, then, with high probability, the 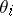 are all equal, so that, in effect, one is working with the model in which the
are all equal, so that, in effect, one is working with the model in which the 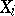 are independent binomial samples with the same success probability. On the other hand, when
are independent binomial samples with the same success probability. On the other hand, when 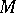 is large, the model (a2) is very close to (a1).
is large, the model (a2) is very close to (a1).
It is interesting to note that when 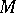 is large and the distribution
is large and the distribution 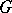 is degenerate, then the measure on
is degenerate, then the measure on 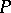 is essentially degenerate, so that one is treating the data from the hospitals as independent. Thus, when the distribution
is essentially degenerate, so that one is treating the data from the hospitals as independent. Thus, when the distribution 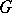 is degenerate, the parameter
is degenerate, the parameter 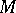 determines the extent to which data from other hospitals is used when making an inference about hospital
determines the extent to which data from other hospitals is used when making an inference about hospital 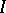 , and in that sense plays the role of tuning parameter in the bias-variance tradeoff of frequentist analysis.
, and in that sense plays the role of tuning parameter in the bias-variance tradeoff of frequentist analysis.
References
| [a1] | C. Antoniak, "Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems" Ann. Statist. , 2 (1974) pp. 1152–1174 |
| [a2] | C.A. Bush, S.N. MacEachern, "A semi-parametric Bayesian model for randomized block designs" Biometrika , 83 (1996) pp. 275–285 |
| [a3] | M. Escobar, M. West, "Bayesian density estimation and inference using mixtures" J. Amer. Statist. Assoc. , 90 (1995) pp. 577–588 |
| [a4] | T.S. Ferguson, "A Bayesian analysis of some nonparametric problems" Ann. Statist. , 1 (1973) pp. 209–230 |
| [a5] | T.S. Ferguson, "Prior distributions on spaces of probability measures" Ann. Statist. , 2 (1974) pp. 615–629 |
| [a6] | J. Sethuraman, "A constructive definition of Dirichlet priors" Statistica Sinica , 4 (1994) pp. 639–650 |
Dirichlet process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_process&oldid=37599