Core in the theory of games

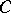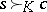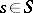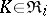The set of all non-dominated outcomes, that is, the set of outcomes such that a domination cannot hold for any outcomes , and coalition . One defines in this respect:

1) The core. The set 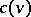of imputations that are not dominated by any other imputation; the core coincides with the set of imputations satisfying 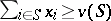for any coalition 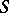. If 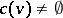and a von Neumann–Morgenstern solution (see Solution in game theory) exists, then is contained in any von Neumann–Morgenstern solution.

2) The kernel. The set 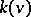of individually rational configurations 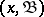(see Stability in game theory) such that the following inequality holds for any :

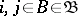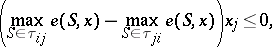where 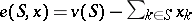and 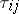is the set of coalitions containing the player 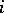and not containing the player 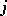. The kernel 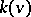is contained in an 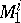-bargaining set.

3) The nucleolus. The minimal imputation 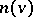relative to the quasi-order 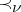defined on the set of imputations by: 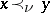if and only if the vector 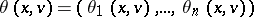, where

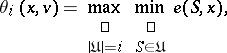lexicographically precedes 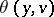. The nucleolus 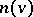exists and is unique for any game with a non-empty set of imputations. In a cooperative game the nucleolus is contained in the kernel.

References

[1]	N.N. Vorob'ev, "The present state of the theory of games" Russian Math. Surveys , 25 : 2 (1970) pp. 77–136 Uspekhi Mat. Nauk , 25 : 2 (1970) pp. 103–107

Comments

The Russian word ( "yadro" ) is the same for all three notions defined above, but these notions may be distinguished by prefixing with the corresponding English letter ( "c-yadroc-yadro" for core, "k-yadrok-yadro" for kernel and "n-yadron-yadro" for nucleolus). These three notions do not share many properties.

See [a1], [a7] for core, [a2] for kernel and [a3] for nucleolus. [a4], [a5] are general references. [a6] deals also with mathematical economics and the role of the concept of the core of a game in that setting.

References

[a1]	O.N. Bondareva, "Certain applications of the methods of linear programming to the theory of cooperative games" Probl. Kibernet , 10 (1963) pp. 119–139 (In Russian)
[a2]	M. Maschler, M. Davis, "The kernel of a cooperative game" Naval Res. Logist. Quart. , 12 (1965) pp. 223–259
[a3]	D. Schmeidler, "The nucleolus of a characteristic function game" SIAM J. Appl. Math. , 17 (1969) pp. 1163–1170
[a4]	G. Owen, "Game theory" , Acad. Press (1982)
[a5]	J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199
[a6]	J. Rosenmüller, "Cooperative games and markets" , North-Holland (1981)
[a7]	L.S. Shapley, "On balanced sets and cores" Naval Res. Logist. Quart. , 14 (1967) pp. 453–460