Banach module
From Encyclopedia of Mathematics
(left) over a Banach algebra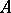 
A Banach space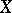 
together with a continuous bilinear operator 
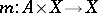defining on 
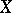the structure of a left module over 
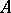in the algebraic sense. A right Banach module and a Banach bimodule over 
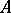are defined in an analogous manner. A continuous homomorphism of two Banach modules is called a morphism. Examples of Banach modules over 
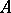include a closed ideal in 
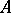and a Banach algebra 
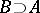. A Banach module over 
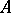that can be represented as a direct factor of Banach modules 
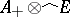, (where 
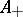is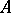 
with an added unit and 
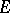is a Banach space and 
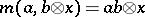) is called projective. Cf. Topological tensor product.
References
| [1] | M.A. Rieffel, "Induced Banach representations of Banach algebras and locally compact groups" J. Funct. Anal. , 1 (1967) pp. 443–491 |
How to Cite This Entry:
Banach module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_module&oldid=36964
Banach module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_module&oldid=36964
This article was adapted from an original article by A.Ya. Khelemskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article