Contraction of a tensor
From Encyclopedia of Mathematics
An operation of tensor algebra that associates with a tensor with components 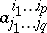 ,
,  , the tensor
, the tensor
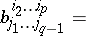 |
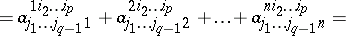 |
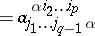 |
(here the contraction is made with respect to the pair of indices 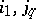 ). The contraction of a tensor with respect to any pair of upper and lower indices is defined similarly. The
). The contraction of a tensor with respect to any pair of upper and lower indices is defined similarly. The 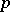 -fold contraction of a tensor that is
-fold contraction of a tensor that is 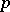 -times covariant and
-times covariant and 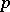 -times contravariant is an invariant. Thus, the contraction of the tensor with components
-times contravariant is an invariant. Thus, the contraction of the tensor with components 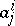 is an invariant
is an invariant 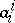 , called the trace of the tensor; it is denoted by
, called the trace of the tensor; it is denoted by 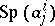 , or
, or 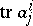 . A contraction of the product of two tensors is a contraction of the product with respect to an upper index of one factor and a lower index of the other.
. A contraction of the product of two tensors is a contraction of the product with respect to an upper index of one factor and a lower index of the other.
Comments
References
| [a1] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
How to Cite This Entry:
Contraction of a tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contraction_of_a_tensor&oldid=36734
Contraction of a tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contraction_of_a_tensor&oldid=36734
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article