Ribaucour curve

A planar curve with curvature radius 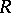at an arbitrary point 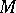proportional to the length of the segment of the normal MP (see Fig.).

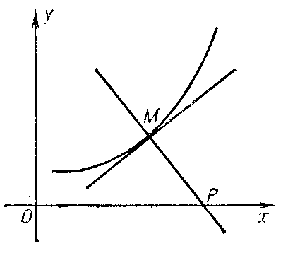
Figure: r081760a

The equation for the Ribaucour curve in Cartesian orthogonal coordinates is

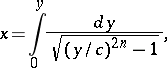where 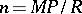. If 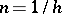( 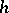is any integer), then a parametric equation for the Ribaucour curve is

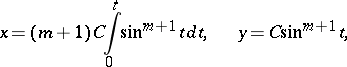where 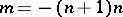. When 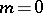, the Ribaucour curve is a circle; when 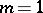, it is a cycloid; when 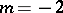, it is a catenary; and when 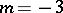, it is a parabola.

The length of an arc of the curve is

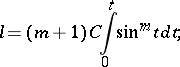and the curvature radius is

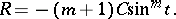This curve was studied by A. Ribaucour in 1880.

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)
[2]	P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian)

References

[a1]	F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971)