Symmetric polynomial
A polynomial $f$ with coefficients in a field or a commutative associative ring $K$ with a unit, which is a symmetric function in its variables, that is, is invariant under all permutations of the variables:
\[ \label{symm} f(x_1,\ldots,x_n) = f(\pi(x_1),\ldots,\pi(x_n)). \]
The symmetric polynomials form the algebra $S(x_1,\ldots,x_n)$ over $K$.
The most important examples of symmetric polynomials are the elementary symmetric polynomials
\[ s_k(x_1,\ldots,x_n) = \sum_{1 \leq i_1 < \ldots < i_k \leq n} x_{i_1} \ldots x_{i_k} \]
and the power sums
\[ p_k(x_1,\ldots,x_n) = x_1^k + \ldots + x_n^k. \]
The latter can be expressed in terms of elementary symmetric polynomials by recurrence formulas, called Newton's formulas:
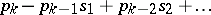 |
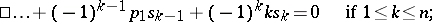 |
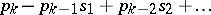 |
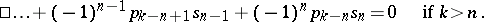 |
For the elementary symmetric polynomials  (
( ) of the roots of an arbitrary polynomial in one variable with leading coefficient 1,
) of the roots of an arbitrary polynomial in one variable with leading coefficient 1, 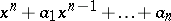 , one has
, one has 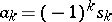 (see Viète theorem).
(see Viète theorem).
The fundamental theorem on symmetric polynomials: Every symmetric polynomial is a polynomial in the elementary symmetric polynomials, and this representation is unique. In other words, the elementary symmetric polynomials are a set of free generators for the algebra 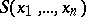 . If the field has characteristic 0, then the polynomials
. If the field has characteristic 0, then the polynomials  also form a set of free generators of this algebra.
also form a set of free generators of this algebra.
A skew-symmetric, or alternating, polynomial is a polynomial 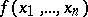 satisfying the relation (1) if
satisfying the relation (1) if 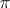 is even and the relation
is even and the relation
 |
if 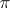 is odd. Any skew-symmetric polynomial can be written in the form
is odd. Any skew-symmetric polynomial can be written in the form 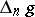 , where
, where 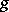 is a symmetric polynomial and
is a symmetric polynomial and
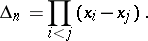 |
This representation is not unique, in view of the relation 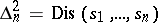 .
.
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
| [2] | A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian) |
| [3] | A.P. Mishina, I.V. Proskuryakov, "Higher algebra. Linear algebra, polynomials, general algebra" , Pergamon (1965) (Translated from Russian) |
Comments
Another important set of symmetric polynomials, which appear in the representations of the symmetric group, are the Schur polynomials (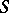 -functions)
-functions) 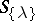 . These are defined for any partition
. These are defined for any partition 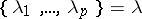 , and include as special cases the above functions, e.g.
, and include as special cases the above functions, e.g. 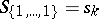 ,
, 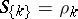 (see, e.g., [a4], Chapt. VI).
(see, e.g., [a4], Chapt. VI).
In general, the discriminant of the polynomial 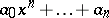 with roots
with roots  is defined as
is defined as 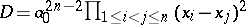 , and satisfies
, and satisfies
 |
with 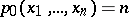 .
.
See Discriminant.
Let 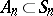 be the alternating group, consisting of the even permutations. The ring of polynomials
be the alternating group, consisting of the even permutations. The ring of polynomials 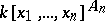 of polynomials over a field
of polynomials over a field 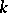 obviously contains the elementary symmetric functions
obviously contains the elementary symmetric functions  and
and 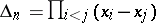 . If
. If 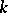 is not of characteristic
is not of characteristic  , the ring of polynomials is generated by
, the ring of polynomials is generated by  and
and 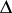 , and the ideal of relations is generated by
, and the ideal of relations is generated by 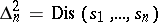 . The condition
. The condition 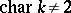 is also necessary for the statement that every skew-symmetric polynomial is of the form
is also necessary for the statement that every skew-symmetric polynomial is of the form 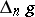 with
with 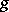 symmetric. More precisely, what is needed for this is that
symmetric. More precisely, what is needed for this is that 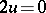 implies
implies 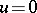 for
for 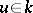 .
.
References
| [a1] | N. Jacobson, "Basic algebra" , 1 , Freeman (1974) |
| [a2] | A.G. Kurosh, "An introduction to algebra" , MIR (1971) (Translated from Russian) |
| [a3] | B.L. van der Waerden, "Algebra" , 1 , Springer (1967) (Translated from German) |
| [a4] | D.E. Littlewood, "The theory of group characters and matrix representations of groups" , Clarendon Press (1950) |
| [a5] | V. Poénaru, "Singularités  en présence de symmétrie" , Springer (1976) pp. 14ff en présence de symmétrie" , Springer (1976) pp. 14ff |
| [a6] | P.M. Cohn, "Algebra" , 1 , Wiley (1982) pp. 181 |
Symmetric polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_polynomial&oldid=36387