Dirichlet character
(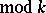 )
)
A function 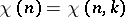 on the set of integers that satisfies the following conditions:
on the set of integers that satisfies the following conditions:
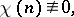 |
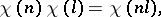 |
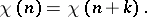 |
In other words, a Dirichlet character  is an arithmetic function that is not identically equal to zero, and that is totally multiplicative and periodic with the period
is an arithmetic function that is not identically equal to zero, and that is totally multiplicative and periodic with the period 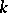 .
.
The concept of a Dirichlet character was introduced by P.G.L. Dirichlet in the context of his study of the law of the distribution of primes in arithmetic progressions. He developed the fundamental principles of the theory of Dirichlet characters [2]–[8], starting from their direct construction.
Let
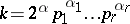 |
be the canonical factorization of 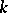 , let
, let  be an integer which is relatively prime to
be an integer which is relatively prime to 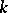 ,
, 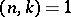 ; set
; set 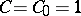 if
if 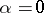 or
or 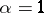 and
and 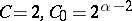 if
if 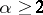 ; let
; let 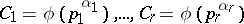 , where
, where 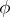 is Euler's function. Further, let
is Euler's function. Further, let 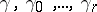 be the system of indices of
be the system of indices of 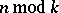 , i.e. the system of least non-negative integers satisfying the congruences
, i.e. the system of least non-negative integers satisfying the congruences
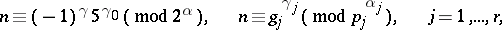 |
where 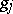 is the smallest primitive root
is the smallest primitive root 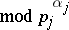 . Let
. Let 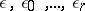 be roots of unity of respective orders
be roots of unity of respective orders 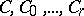 . The function
. The function
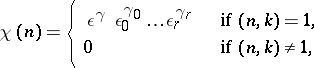 |
defined on the set of all natural numbers, is a Dirichlet character 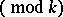 . Inspection of all possible choices of
. Inspection of all possible choices of 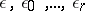 yields
yields
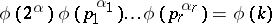 |
different functions 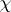 , i.e. Dirichlet characters
, i.e. Dirichlet characters 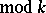 . The character with
. The character with 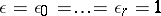 is known as the principal character and is denoted by
is known as the principal character and is denoted by 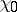 :
:
 |
For any natural numbers  ,
, 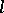 and
and 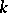 , one has
, one has
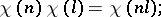 |
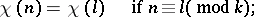 |
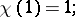 |
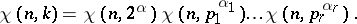 |
If  is a Dirichlet character
is a Dirichlet character 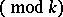 , the complex conjugate function
, the complex conjugate function 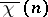 is also a Dirichlet character
is also a Dirichlet character 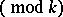 ; and
; and
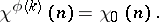 |
The smallest positive number  that satisfies the equation
that satisfies the equation 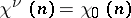 is called the order of the Dirichlet character. For
is called the order of the Dirichlet character. For 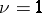 there exists only the character
there exists only the character 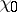 . If
. If  ,
, 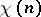 may assume the values 0 and
may assume the values 0 and 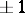 only; such Dirichlet characters are known as real or quadratic. If
only; such Dirichlet characters are known as real or quadratic. If 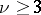 , the Dirichlet character is said to be complex.
, the Dirichlet character is said to be complex. 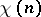 is called even or odd, depending on whether
is called even or odd, depending on whether 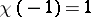 or
or 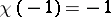 . The principal properties of Dirichlet characters are expressed by the formulas
. The principal properties of Dirichlet characters are expressed by the formulas
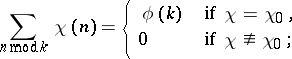 |
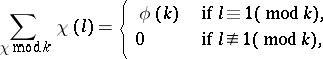 |
where in the first formula  ranges over a complete residue system
ranges over a complete residue system  , and
, and 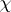 in the second formula ranges over all
in the second formula ranges over all 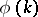 characters
characters 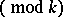 .
.
If 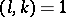 , the formula
, the formula
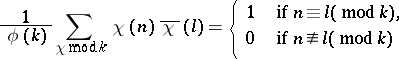 |
holds. It is called the orthogonality property of Dirichlet characters. It is one of the fundamental formulas for Dirichlet characters and is used in investigating various types of arithmetic progressions 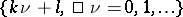 . In the theory and applications of Dirichlet characters other important concepts are the conductor of a character and primitive characters. Let
. In the theory and applications of Dirichlet characters other important concepts are the conductor of a character and primitive characters. Let 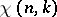 be an arbitrary non-principal character
be an arbitrary non-principal character  . If, for the values
. If, for the values  satisfying
satisfying  , the number
, the number 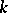 is the smallest period of
is the smallest period of 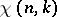 ,
, 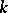 is said to be the conductor of the character
is said to be the conductor of the character 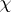 , while the character
, while the character 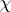 itself is known as a primitive character
itself is known as a primitive character  . Otherwise there exists a unique number
. Otherwise there exists a unique number 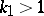 dividing
dividing 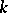 ,
, 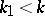 , and a primitive character
, and a primitive character 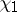 (
(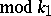 ) such that
) such that
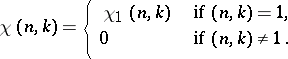 |
In such a case 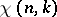 is said to be the imprimitive character of
is said to be the imprimitive character of 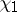 (
(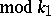 ), and one says that
), and one says that 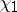 induces
induces 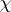 . In this way many problems on characters are reduced to problems on primitive characters.
. In this way many problems on characters are reduced to problems on primitive characters.
A character 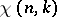 is primitive if and only if for any
is primitive if and only if for any 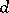 that divides
that divides 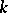 ,
, 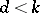 , there exists an
, there exists an  that satisfies the conditions
that satisfies the conditions
 |
The analytic theory extensively employs Gauss sums, which are defined for 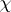 (
(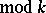 ) by the equality:
) by the equality:
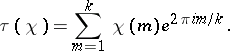 |
For a primitive character  (
(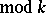 ) one has
) one has
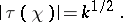 |
Moreover, the following expansion of 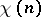 is valid:
is valid:
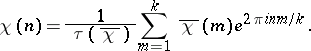 |
One of the principal problems in the theory of Dirichlet characters is the problem of estimating character sums
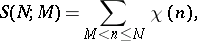 |
where 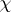 is a non-principal character
is a non-principal character 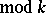 . One has Vinogradov's estimate
. One has Vinogradov's estimate
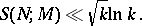 |
It was found [7] that
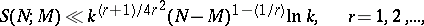 |
where 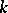 is a prime. If
is a prime. If 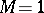 ,
, 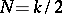 , there exists [8] an infinite sequence of numbers
, there exists [8] an infinite sequence of numbers 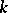 which are modules of a primitive real character
which are modules of a primitive real character 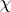 for which
for which
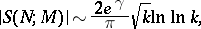 |
where 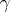 is the Euler constant. This asymptotic equation shows that it is not possible, in general, to strengthen the previous estimates essentially. However, there exists Vinogradov's hypothesis according to which for any
is the Euler constant. This asymptotic equation shows that it is not possible, in general, to strengthen the previous estimates essentially. However, there exists Vinogradov's hypothesis according to which for any 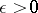 ,
, 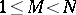 ,
,
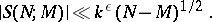 |
A proof of this hypothesis would permit one to solve several major problems in number theory.
The theory of Dirichlet characters forms the basis of the theory of Dirichlet 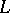 -functions (cf. Dirichlet
-functions (cf. Dirichlet  -function), and is a special case of the general theory of characters of Abelian groups (cf. Character of a group).
-function), and is a special case of the general theory of characters of Abelian groups (cf. Character of a group).
References
| [1] | P.G.L. Dirichlet, "Vorlesungen über Zahlentheorie" , Vieweg (1894) |
| [2] | I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) |
| [3] | A.A. Karatsuba, "Fundamentals of analytic number theory" , Moscow (1975) (In Russian) |
| [4] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
| [5] | N.G. Chudakov, "Introductions to the theory of Dirichlet  -functions" , Moscow-Leningrad (1947) (In Russian) -functions" , Moscow-Leningrad (1947) (In Russian) |
| [6] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
| [7] | D.A. Burgess, "Dirichlet characters and polynomials" Proc. Steklov Inst. Math. , 132 (1975) pp. 234–236 Trudy Mat. Inst. Steklov. , 132 (1973) pp. 203–205 |
| [8] | A.F. Lavrik, "A method for estimating double sums with real quadratic character, and applications" Math. USSR-Izv. , 5 : 6 (1971) pp. 1195–1214 Izv. Akad. Nauk SSSR Ser. Mat. , 35 : 6 (1971) pp. 1189–1207 |
Dirichlet character. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_character&oldid=36176