Van der Waerden theorem

on arithmetic progressions

Given natural numbers , there exists a number such that if 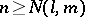and 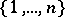is partitioned into 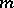sets, then at least one set contains 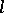terms in arithmetic progression [a1]. Another, equivalent, non-finitary, formulation is as follows. Let 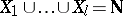be a finite partition of the natural numbers; then at least one 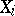contains arithmetic progressions of arbitrary length. The result was conjectured by A. Baudet. Let be a set of natural numbers and let be its upper asymptotic density. When discussing van der Waerden's theorem stated above, P. Erdös and P. Turán conjectured that if 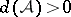, then 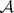contains arbitrary long arithmetic progressions; [a2].

Let 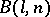be a maximally large subset of 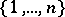which contains no elements in arithmetic progression. Let 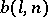be the number of elements in a 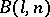. Then Szemerédi's theorem, [a3], says that 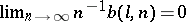. This implies the Erdös–Turán conjecture. Another proof of Szemerédi's theorem was given by H. Furstenberg, based on ideas from ergodic theory, [a4].

For a personal historical account of the van der Waerden theorem see [a6].

References

[a1]	B.L. van der Waerden, "Beweis einer Baudetschen Vermutung" Nieuw Arch. Wisk. , 15 (1927) pp. 212–216
[a2]	P. Erdös, P. Turán, "On some sequences of integers" J. London Math. Soc. , 11 (1936) pp. 261–264
[a3]	E. Szemerédi, "On sets of integers containing no 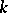-elements in arithmetic progression" Acta Arithm. , 27 (1975) pp. 199–245
[a4]	H. Furstenberg, "Ergodic behaviour of diagonal measures and a theorem of Szemerédi on arithmetic progressions" J. d'Anal. Math. , 31 (1977) pp. 204–256
[a5]	H. Furstenberg, "Recurrence in ergodic theory and combinatorial number theory" , Princeton Univ. Press (1981)
[a6]	A.Ya. Khinchin, "Three pearls of number theory" , Graylock (1952) (Translated from Russian)