Everett interpolation formula
A method of writing the interpolation polynomial obtained from the Gauss interpolation formula for forward interpolation at 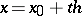 with respect to the nodes
with respect to the nodes 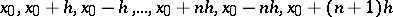 , that is,
, that is,
 |
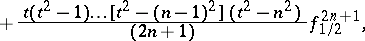 |
without finite differences of odd order, which are eliminated by means of the relation
 |
Adding like terms yields Everett's interpolation formula
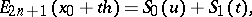 | (1) |
where 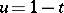 and
and
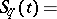 | (2) |
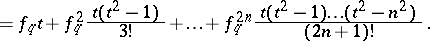 |
Compared with other versions of the interpolation polynomial, formula (1) reduces approximately by half the amount of work required to solve the problem of table condensation; for example, when a given table of the values of a function at 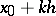 is to be used to draw up a table of the values of the same function at
is to be used to draw up a table of the values of the same function at 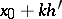 ,
, 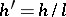 , where
, where 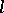 is an integer, the values
is an integer, the values 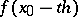 for
for 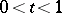 are computed be means of the formula
are computed be means of the formula
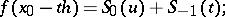 |
and 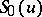 is used to find both values
is used to find both values 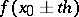 .
.
In manual calculation, in the case 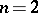 it is advisable to approximate the coefficient of
it is advisable to approximate the coefficient of 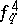 in (2) by
in (2) by
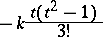 |
and instead of 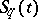 to compute
to compute
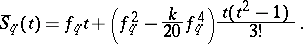 |
The parameter 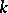 can be chosen, for example, from the condition that the principal part of
can be chosen, for example, from the condition that the principal part of
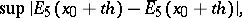 |
where
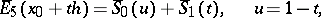 |
has a minimum value. In this case 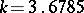 .
.
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
Comments
References
| [a1] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126 |
| [a2] | A.J. Thomson, "Table of the coefficients of Everett's central differrence interpolation formula" , Cambridge Univ. Press (1965) |
Everett interpolation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Everett_interpolation_formula&oldid=36054