Lie differential

of a tensor field 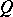in the direction of a vector field

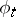The principal linear part of increment of under its transformation induced by the local one-parameter group of transformations of the manifold generated by 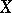. The Lie differential 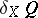of a tensor field 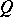in the direction of a vector field 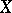is equal to 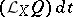, where 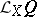is the Lie derivative of in the direction of .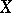

The concept of a Lie differential admits the following physical interpretation. If a one-parameter transformation group 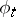of a domain of the Euclidean space describes the stationary flow of a liquid with velocity field , 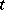is time and is a tensor field that describes some characteristic of the liquid (the deformation velocity tensor, stress tensor, density, etc.), then the Lie differential 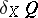describes the principal linear part of variation with time of 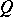from the point of view of an observer moving with the liquid, that is, in Lagrange variables.