Verbal congruence
From Encyclopedia of Mathematics
A congruence on an algebra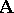 
which is expressible as the intersection of all congruences on 
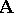whose factor algebras belong to some fixed variety of 
-algebras. A congruence 
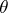on an arbitrary algebraic system 
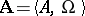is said to be verbal if there exists a variety 
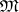of 
-systems for which the canonical mapping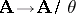 
is universal amongst the morphisms from 
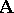to algebras in 
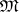. A verbal congruence is a fully-characteristic congruence. If 
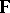is a free 
-system in some variety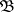 
, then, conversely, any fully-characteristic congruence 
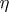in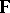 
is a verbal congruence with respect to the variety 
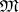generated by the factor system 
.
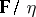References
| [1] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
Comments
Cf. also Universal property; Congruence (in algebra).
How to Cite This Entry:
Verbal congruence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Verbal_congruence&oldid=35793
Verbal congruence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Verbal_congruence&oldid=35793
This article was adapted from an original article by D.M. Smirnov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article