Legendre symbol

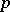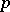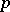An arithmetic function of the numbers and , defined for odd prime numbers and integers not divisible by . The Legendre symbol is denoted by . The Legendre symbol 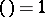if the congruence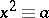 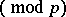is solvable; otherwise, 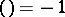. The Legendre symbol is sometimes defined for numbers divisible by by putting 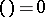in this case. The Legendre symbol has the following properties:

1) if 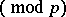, then ;

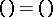2) ;

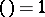3) ;

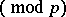4) ;

5) ;

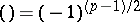6) ;

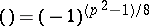7) if and 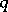are odd prime numbers, then

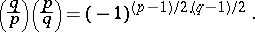The last fact, first proved by C.F. Gauss (1796), is called the quadratic reciprocity law. The above properties make it possible to calculate the Legendre symbol easily, without resorting to solving congruences. For example,

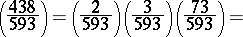The calculation of the Legendre symbol is facilitated still more by the use of the Jacobi symbol. For fixed 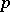the Legendre symbol is a real character of the multiplicative group of residue classes modulo 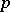(cf. Character of a group).

It was introduced by A.M. Legendre in 1785.

References

[1]	I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)

References

[a1]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979)