Fractal dimension
From Encyclopedia of Mathematics
A, possibly non-integer valued, dimension concept. Let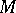 
be a metric space and 
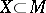a bounded subset. For each 
let 
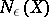be the minimal number of balls of radius 
necessary to cover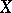 
. Then
 |
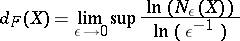is the fractal dimension of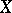 
. It has also been called the capacity, the Mandelbrot dimension or the Shnirel'man–Kolmogorov dimension of 
.
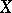One has
 |
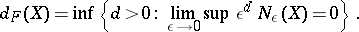If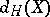 
denotes the Hausdorff dimension of 
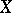, then 
.
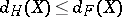References
| [a1] | B.B. Mandelbrot, "Form, chance and dimension" , Freeman (1977) |
How to Cite This Entry:
Fractal dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractal_dimension&oldid=35687
Fractal dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractal_dimension&oldid=35687