Ergodic theory, non-commutative

A branch of the theory of operator algebras in which one studies automorphisms of 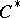-algebras (cf. 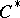-algebra) from the point of view of ergodic theory.

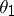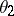The range of questions considered in non-commutative ergodic theory and the results obtained so far (1984) can be basically divided into three groups. To the first group belong results connected with the construction of a complete system of invariants for outer conjugacy. (Two automorphisms and are called outer conjugate if there exists an automorphism 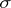such that 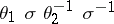is an inner automorphism.) The corresponding classification problem has been solved (see [1]) for approximately-finite factors (cf. Factor) of type II and type 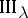, 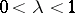(see [2]).

To the second group belong articles devoted to the study of properties of equilibrium states (by a state in an algebra one means a positive linear normalized functional on the algebra) which are invariant under a one-parameter group of automorphisms. In particular, one considers questions of existence and uniqueness of Gibbs states (see [3]). Closely related to this group of problems are investigations on non-commutative generalizations of ergodic theorems (see, for example, [4], [5]).

The third group consists of results concerning the entropy theory of automorphisms. For automorphisms of finite 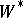-algebras (see von Neumann algebra) an invariant has been constructed [6] that generalizes the entropy of a metric dynamical system. The entropy of automorphisms of an arbitrary 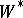-algebra with respect to a state 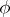has been investigated [7].

References

[1]	A. Connes, "Outer conjugacy classes of automorphisms of factors" Ann. Sci. Ecole. Norm. Sup. , 8 (1975) pp. 383–419
[2]	V.Ya. Golodets, "Modular operators and asymptotic commutativity in Von Neumann algebras" Russian Math. Surveys , 33 : 1 (1978) pp. 47–106 Uspekhi Mat. Nauk , 33 : 1 (1978) pp. 43–94
[3]	H. Araki, "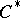-algebras and applications to physics" , Lect. notes in math. , 650 , Springer (1978) pp. 66–84
[4]	Ya.G. Sinai, V.V. Anshelevich, "Some problems of non-commutative ergodic theory" Russian Math. Surveys , 31 : 4 (1976) pp. 157–174 Uspekhi Mat. Nauk , 31 : 4 (1976) pp. 151–167
[5]	E.C. Lance, "Ergodic theorems for convex sets and operator algebras" Invent. Math. , 37 (1976) pp. 201–214
[6]	A. Connes, E. Størmer, "Entropy for automorphisms of 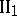Von Neumann algebras" Acta Math. , 134 (1975) pp. 289–306
[7]	A.M. Stepin, A.G. Shukhov, "The centralizer of diagonable states and entropies of automorphisms of 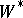-algebras" Soviet Math. (Vuz) , 26 : 8 (1982) pp. 61–71 Izv. Vuzov. Mat. , 8 (1982) pp. 52–60