Semi-ring
From Encyclopedia of Mathematics
A non-empty set with two associative binary operations 
and 
, satisfying the distributive laws
 |
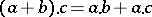and
 |
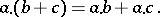In most cases one also assumes that the addition is commutative and that there exists a zero 
such that 
for every 
. The most important examples of semi-rings are rings and distributive lattices (cf. Ring; Distributive lattice). If there is a multiplicative identity 1, the two classes are combined by the condition
 |
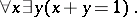The non-negative integers with the usual operations provide an example of a semi-ring that does not satisfy this condition.
How to Cite This Entry:
Semi-ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-ring&oldid=35628
Semi-ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-ring&oldid=35628
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article