BCH-algebra

A variant of a BCI-algebra. One can define it by taking some of the axioms for a BCI-algebra and some of the important properties of a BCI-algebra. Specifically, a BCH-algebra is a non-empty set 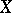with a constant and a binary relation satisfying the following axioms:

1) ;

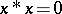2) if 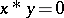and 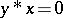, then ;

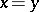3) 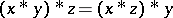. Clearly a BCI-algebra is a BCH-algebra; however, the converse is not true. While some work has been done on such algebras, generally they have not been as extensively investigated as BCI-algebras.

References

[a1]	Qing-ping Hu, Xin Li, "On BCH-algebras" Math. Seminar Notes (Kobe University) , 11 (1983) pp. 313–320
[a2]	Y. Imai, K. Iséki, "On axiom systems of propositional calculi, XIV" Proc. Japan Acad. Ser. A Math. Sci. , 42 (1966) pp. 19–22
[a3]	K. Iséki, "An algebra related with a propositional calculus" Proc. Japan Acad. Ser. A, Math. Sci. , 42 (1966) pp. 26–29