Closed-graph theorem
From Encyclopedia of Mathematics
Let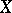 
and 
be complete metric linear spaces with translation-invariant metrics, i.e.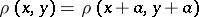 
, 
(similarly for 
), and let 
be a linear operator from 
to 
. If the graph 
of this operator is a closed subset of the Cartesian product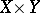 
, then 
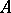is continuous. The closed-graph theorem has various generalizations; for example: a linear mapping with closed graph from a separable barrelled space into a perfectly-complete space is continuous. Closely related theorems are the open-mapping theorem and Banach's homeomorphism theorem.
References
| [1] | W. Rudin, "Functional analysis" , McGraw-Hill (1979) |
| [2] | A.P. Robertson, W.S. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964) |
Comments
Cf. also Open-mapping theorem (also for the Banach homeomorphism theorem).
How to Cite This Entry:
Closed-graph theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed-graph_theorem&oldid=35500
Closed-graph theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed-graph_theorem&oldid=35500
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article