Bimodule

double module

An Abelian group that is a left module over a ring and a right module over a ring , and is such that for all , , . One says that this is the situation , or that is an 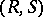-bimodule. The bimodule 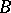may be regarded as a left 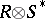-module, where 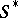is the ring which is dually isomorphic (anti-isomorphic) to 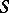, while 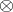denotes the tensor product over the ring of integers, and 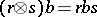. 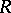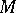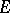For every left -module one has the situation , where is the ring of endomorphisms of 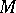. Any ring 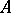can be given the natural structure of an 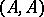-bimodule.

Comments

A bimodule morphism is a mapping from a bimodule 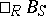into a bimodule 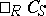that is left 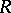-linear and right 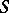-linear. The category of 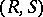-bimodules with bimodule morphisms is a Grothendieck category.

The centre of an 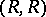-bimodule (also called an 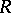-bimodule) 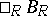is defined to be the set 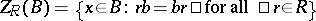. Clearly 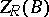is a two-sided 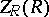-module.