Inner automorphism
of a group 
An automorphism 
such that
 |
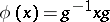for a certain fixed element 
. The set of all inner automorphisms of 
forms a normal subgroup in the group of all automorphisms of 
; this subgroup is isomorphic to 
, where 
is the centre of 
(cf. Centre of a group). Automorphisms that are not inner are called outer automorphisms.
Other relevant concepts include those of an inner automorphism of a monoid (a semi-group with a unit element) and an inner automorphism of a ring (associative with a unit element), which are introduced in a similar way using invertible elements.
Comments
Let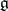 
be a Lie algebra and 
an element of 
for which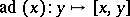 
is nilpotent. Then
 |
defines an automorphism of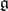 
. Such an automorphism is called an inner automorphism of 
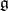. More generally, the elements in the group 
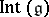generated by them are called inner automorphisms. It is a normal subgroup of 
.
If 
is a real or complex Lie group with semi-simple Lie algebra, then the inner automorphisms constitute precisely the identity component of the group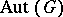 
of automorphisms of 
.
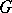References
| [a1] | M. Hall jr., "The theory of groups" , Macmillan (1959) |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
| [a3] | J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) |
Inner automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inner_automorphism&oldid=35114