Conjunctive normal form
From Encyclopedia of Mathematics
A propositional formula of the form
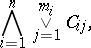 | (*) |
where each  ,
,  ;
;  , is either an atomic formula (a variable or constant) or the negation of an atomic formula. The conjunctive normal form (*) is a tautology if and only if for any
, is either an atomic formula (a variable or constant) or the negation of an atomic formula. The conjunctive normal form (*) is a tautology if and only if for any  one can find both formulas
one can find both formulas  and
and  among the
among the  , for some atomic formula
, for some atomic formula  . Given any propositional formula
. Given any propositional formula  , one can construct a conjunctive normal form
, one can construct a conjunctive normal form 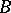 equivalent to it and containing the same variables and constants as
equivalent to it and containing the same variables and constants as  . This
. This 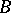 is called the conjunctive normal form of
is called the conjunctive normal form of 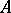 .
.
Comments
The dual of a conjunctive normal form is a disjunctive normal form. Both are also used in the theory of Boolean functions (cf. Boolean functions, normal forms of).
How to Cite This Entry:
Conjunctive normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjunctive_normal_form&oldid=35077
Conjunctive normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjunctive_normal_form&oldid=35077
This article was adapted from an original article by S.K. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article