Morita equivalence

An equivalence relation on the class of all rings (cf. Ring) defined as follows: Two rings and are called Morita equivalent if the categories of left (right) - and -modules are equivalent. The most important examples of Morita-equivalent rings are: a ring and the ring of all -matrices over it. In order that there is Morita equivalence between two rings and it is necessary and sufficient that in the category of left -modules there is a finitely-generated projective generator 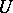such that its ring of endomorphisms is isomorphic to 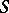. The left 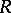-module is put in correspondence with the left 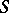-module 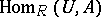. Among the properties preserved by transition to a Morita-equivalent ring are the properties of being: Artinian, Noetherian, primary, simple, classically semi-simple, regular, self-injective, hereditary, and primitive.

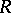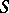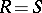Alongside with Morita equivalence one considers Morita duality, relating some subcategories of the categories of left -modules and right -modules (mostly the subcategories of finitely-generated modules). However, the very existence of such a duality places definite restrictions on the rings and . In particular, for this implies that 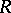is a quasi-Frobenius ring.

The general concept of Morita equivalence was developed by K. Morita [1].

References

[1]	K. Morita, Sci. Reports Tokyo Kyoiku Dajkagu A , 6 (1958) pp. 83–142
[2]	H. Bass, "Algebraic 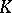-theory" , Benjamin (1968)
[3]	C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1981–1976)
[4]	P. Cohn, "Morita equivalence and duality" , London (1976)

Comments

For generating objects of categories see also Generator of a category.

Let 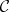and 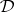be categories. A duality is a pair of contravariant functors 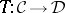and such that 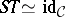, , 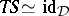where 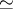denotes natural equivalence (functorial isomorphism) and is the identity functor on .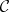

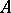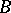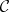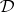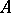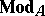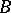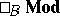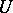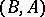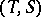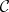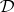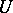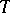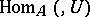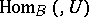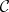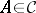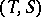Let and be rings and let and be full subcategories of the categories of right -modules and left -modules , respectively (cf. Module). Let be a bimodule. A duality between and is called a -duality or Morita duality if and are, respectively, naturally equivalent to and . A theorem of Morita says that if and are Abelian full subcategories with and , then any duality between and is a -duality with .