Normally-imbedded subspace
From Encyclopedia of Mathematics
A subspace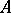 
of a space 
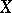such that for every neighbourhood 
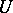of it in 
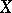there is a set 
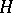that is the union of a countable family of sets closed in 
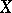and with 
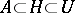. If 
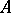is normally imbedded in 
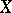and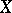 
is normally imbedded in 
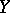, then 
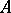is normally imbedded in 
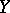. A normally-imbedded subspace of a normal space is itself normal in the induced topology, which explains the name. Final compactness of a space is equivalent to its being normally imbedded in some (and hence in any) compactification of this space. Quite generally, a normally-imbedded subspace of a finally-compact space is itself finally compact.
References
| [1] | Yu.M. Smirnov, "On normally-imbedded sets of normal spaces" Mat. Sb. , 29 (1951) pp. 173–176 (In Russian) |
Comments
A finally-compact space is the same as a Lindelöf space.
How to Cite This Entry:
Normally-imbedded subspace. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normally-imbedded_subspace&oldid=34634
Normally-imbedded subspace. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normally-imbedded_subspace&oldid=34634
This article was adapted from an original article by A.V. Arkhangel'skii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article