Secant
From Encyclopedia of Mathematics
One of the trigonometric functions:
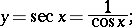 |
another notation is 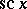 . Its domain of definition is the whole real line apart from the points
. Its domain of definition is the whole real line apart from the points
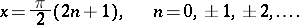 | (*) |
The secant is an unbounded even 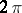 -periodic function. The derivative of the secant is
-periodic function. The derivative of the secant is
 |
The indefinite integral of the secant is
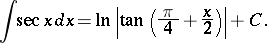 |
The secant can be expanded in a series:
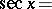 |
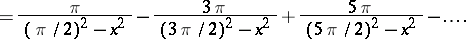 |
Comments
The series expansion is valid in the domain of definition of 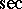 , i.e. not for the points (*).
, i.e. not for the points (*).
References
| [a1] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
| [a2] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1965) pp. §4.3 |
How to Cite This Entry:
Secant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Secant&oldid=34482
Secant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Secant&oldid=34482
This article was adapted from an original article by Yu.A. Gor'kov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article