Ideal series
of a semi-group 
A sequence of sub-semi-groups
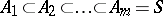 | (*) |
such that 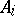 is a (two-sided) ideal of
is a (two-sided) ideal of 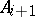 ,
, 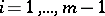 . The sub-semi-group
. The sub-semi-group 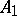 and the Rees factor semi-groups
and the Rees factor semi-groups 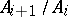 (see Semi-group) are called the factors of the series (*). Two ideal series are said to be isomorphic if a one-to-one correspondence can be established between the factors such that corresponding factors are isomorphic. An ideal series
(see Semi-group) are called the factors of the series (*). Two ideal series are said to be isomorphic if a one-to-one correspondence can be established between the factors such that corresponding factors are isomorphic. An ideal series
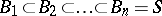 |
is said to be a refinement of (*) if every 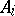 occurs among the
occurs among the 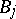 . An ideal series is a composition series if it does not have proper refinements. Any two ideal series of a semi-group have isomorphic refinements; in particular, in a semi-group having a composition series all such series are isomorphic (the analogue of the theorems of Schreier and Jordan–Hölder for normal series in groups, see [1], [2]). An ideal series is a chief series if its terms are ideals in the whole semi-group and if it has no proper refinements consisting of ideals of the semi-group. If a semi-group has a composition series, then it also has a chief series; the converse is false. In a semi-group with a chief series, its factors are isomorphic to the chief factors (cf. Principal factor) of
. An ideal series is a composition series if it does not have proper refinements. Any two ideal series of a semi-group have isomorphic refinements; in particular, in a semi-group having a composition series all such series are isomorphic (the analogue of the theorems of Schreier and Jordan–Hölder for normal series in groups, see [1], [2]). An ideal series is a chief series if its terms are ideals in the whole semi-group and if it has no proper refinements consisting of ideals of the semi-group. If a semi-group has a composition series, then it also has a chief series; the converse is false. In a semi-group with a chief series, its factors are isomorphic to the chief factors (cf. Principal factor) of 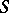 .
.
As for normal series in groups, the concepts mentioned above (as well as their properties) naturally generalize to the case of infinite systems of nested sub-semi-groups. In particular, an ascending ideal series in a semi-group 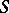 is a totally ordered sequence
is a totally ordered sequence
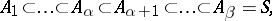 |
where at limit points there stand the unions of the preceding members, and 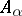 is an ideal of
is an ideal of 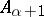 for all
for all 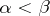 .
.
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [2] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
Ideal series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ideal_series&oldid=34405