Tangent flow
A flow in the space  of orthonormal
of orthonormal  -frames of an
-frames of an  -dimensional Riemannian manifold
-dimensional Riemannian manifold  , having the following property. Let
, having the following property. Let  be an arbitrary trajectory of the flow; by definition of the space
be an arbitrary trajectory of the flow; by definition of the space 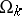 ,
,  is some
is some  -frame
-frame  at some point
at some point  (that is, in the tangent space to
(that is, in the tangent space to  at this point). It is required that
at this point). It is required that  (a variant: it is required that the moving frame of the parametrized curve
(a variant: it is required that the moving frame of the parametrized curve 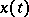 in
in 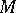 has as its first
has as its first 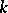 vectors precisely
vectors precisely  ). To obtain interesting results on tangent flows it is necessary to impose various extra conditions. The results obtained generalize certain of the properties of a geodesic flow (which is a particular case of a tangent flow, when
). To obtain interesting results on tangent flows it is necessary to impose various extra conditions. The results obtained generalize certain of the properties of a geodesic flow (which is a particular case of a tangent flow, when  and the covariant derivative
and the covariant derivative  ). See [1], [2].
). See [1], [2].
Various types of flow in the tangent space to some manifold  (or, if it is supposed that
(or, if it is supposed that  is endowed with a Riemannian or a Finsler metric, in the space of unit tangent vectors) were sometimes called tangent flows. For example, a spray (generally, a system of equations of the second order) on
is endowed with a Riemannian or a Finsler metric, in the space of unit tangent vectors) were sometimes called tangent flows. For example, a spray (generally, a system of equations of the second order) on  and the variational equation of a flow on
and the variational equation of a flow on 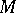 were called tangent flows. But this terminology did not achieve wide application. More customary terminology has since been used.
were called tangent flows. But this terminology did not achieve wide application. More customary terminology has since been used.
References
| [1] | V.I. Arnol'd, "Some remarks on flows of line elements and frames" Soviet Math. Dokl. , 2 (1961) pp. 562–564 Dokl. Akad. Nauk SSSR , 138 : 2 (1961) pp. 255–257 |
| [2] | V.I. Arnol'd, "Remarks on winding numbers" Sibirsk. Mat. Zh. , 2 : 6 (1961) pp. 807–813 (In Russian) |
Tangent flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent_flow&oldid=34400