Duel
A game involving the choice of the moment of time describing the following type of conflict. Two opponents may shoot at each other during a certain period of time, while the weapons at their disposal have only a limited number of rounds of ammunition. The strategies of the players are the moments of time chosen for firing. The pay-off function is defined as the mathematical expectation of a certain random variable which assumes a finite number of values, corresponding to the results of the duel. Depending on the information about the activities of the opponent, duels may be noisy or noise-less (silent). For instance, if each player can fire one shot, and if that shot must be fired in the interval 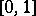 , if the accuracy functions (i.e. the hit probabilities of the players I and II) are
, if the accuracy functions (i.e. the hit probabilities of the players I and II) are 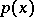 and
and  , respectively; then, if player I gains 1 point if he kills II, loses 1 point if he is killed himself, and the gain is 0 in all other cases, the pay-off functions
, respectively; then, if player I gains 1 point if he kills II, loses 1 point if he is killed himself, and the gain is 0 in all other cases, the pay-off functions 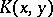 are:
are:
in a noisy duel
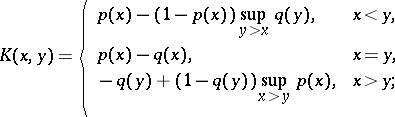 |
in a silent duel
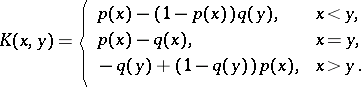 |
The duels under study include duels in which the opponents have several shots at their disposal or are permitted to expend the available resources in a continuous manner.
References
| [1] | S. Karlin, "Mathematical methods in the theory of games, programming and economics" , Addison-Wesley (1959) |
Duel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Duel&oldid=34396