Rotation of a vector field

on a plane

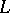One of the characteristics of a vector field that are invariant under homotopy. Let be a vector field on a domain of the Euclidean plane and let be the angle between and some fixed direction; the rotation of will then be the increment of the angle when going around a closed oriented curve along which , divided by . 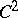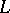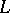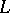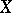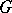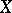For instance, if is a smooth curve of class , the rotation of the field (or ) tangent to (or normal to ) along is equal to the total curvature of divided by ; if is a vector field (with or without isolated singular points) on a domain , with Jordan boundary , then the rotation of on 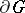is equal to the sum of the indices of the singular points of 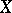in the closure of 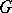(cf. Singular point, index of a). The rotation of a vector field remains unchanged during a homotopic deformation of 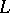which does not pass through the singular points of .

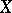A generalization consists of the concept of the index of a vector field on an -dimensional manifold 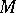, at an isolated point 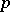of . It is defined as the degree of 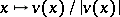, as a mapping from a small sphere around 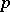to the unit sphere (cf. Degree of a mapping). It is related to the Euler characteristic. See also Poincaré theorem; Kronecker formula.

Comments

Cf. also Rotation number of a curve, which is the rotation of the unit tangent vector field of the curve along that curve.

References

[a1]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French)
[a2]	W. Greub, S. Halperin, R. Vanstone, "Connections, curvature, and cohomology" , 1–3 , Acad. Press (1972)
[a3]	A. Pollack, "Differential topology" , Prentice-Hall (1974)