Content
A set  has (Lebesgue) content zero if for all
has (Lebesgue) content zero if for all  there is a finite set of closed rectangles
there is a finite set of closed rectangles  such that
such that  and
and  , where
, where  is Lebesgue measure.
is Lebesgue measure.
More generally, let  be a space equipped with a ring
be a space equipped with a ring  of subsets such that
of subsets such that  (
( need not be a
need not be a 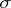 -ring and
-ring and  need not be in
need not be in 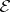 ). Let a function
). Let a function  on
on  be given such that
be given such that  for all
for all 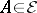 ,
,  for at least one
for at least one  and such that
and such that  is additive on
is additive on  . Such a function is called a content, and
. Such a function is called a content, and  is the content of
is the content of  .
.
Define a rectangle 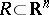 as a product
as a product  , where the
, where the 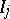 are bounded closed, open or half-closed intervals, and let
are bounded closed, open or half-closed intervals, and let  , where
, where  is the length of the interval
is the length of the interval 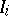 . Define an elementary set in
. Define an elementary set in  to be a finite union of rectangles. Let
to be a finite union of rectangles. Let 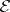 be the collection of all elementary sets. Each
be the collection of all elementary sets. Each 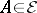 can be written as a finite disjoint union of rectangles
can be written as a finite disjoint union of rectangles  ; then define
; then define  . This defines a content on
. This defines a content on 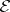 called Jordan content.
called Jordan content.
Given a content 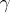 on
on  and any
and any 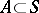 ,
, 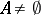 , one defines
, one defines
 |
where the infimum is taken over all finite sums such that  ,
,  ; also one sets
; also one sets  . This defines an outer measure on
. This defines an outer measure on 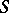 .
.
References
| [a1] | J.F. Randolph, "Basic real and abstract analysis" , Acad. Press (1968) |
| [a2] | M.M. Rao, "Measure theory and integration" , Interscience (1987) |
Content. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Content&oldid=34243