Limit of star-likeness
From Encyclopedia of Mathematics
exact radius of star-likeness, bound of star-likeness
The least upper bound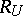 
of the radii of discs 
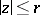, where 
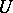is some class of functions 
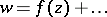that are regular and univalent in 
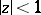, such that the functions from 
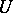on the disc 
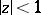map the discs 
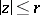onto star-like domains (cf. Star-like domain) about the point 
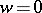. Any number 
in the interval 
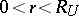is called a radius of star-likeness of the class 
.
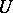The limit of star-likeness is usually found by using the following criterion of star-likeness: A disc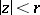 
is mapped onto a star-like domain by 
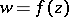if and only if on 
,
 |
or, equivalently,
 |
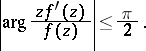The limit of star-likeness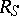 
of the class 
of all functions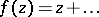 
that are regular and univalent in the disc 
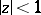is equal to 
.
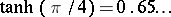References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Comments
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
How to Cite This Entry:
Limit of star-likeness. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit_of_star-likeness&oldid=34115
Limit of star-likeness. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit_of_star-likeness&oldid=34115
This article was adapted from an original article by E.G. Goluzina (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article