Monotone operator

One of the notions in non-linear functional analysis.

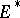Let be a Banach space, its dual, and let be the value of a linear functional 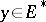at an element 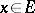. An operator 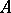, in general non-linear and acting from 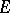into 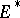, is called monotone if

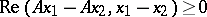(1)

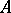for any . An operator is called semi-continuous if for any 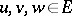the numerical function 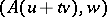is continuous in 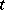. An example of a semi-continuous monotone operator is the gradient of a convex Gâteaux-differentiable functional. Many functionals in variational calculus are convex and hence generate monotone operators; they are useful in the solution of non-linear integral equations and were in fact first applied there.

Various applications of monotone operators in questions regarding the solvability of non-linear equations are based on the following theorem (see [1], [2]). Let be a reflexive Banach space (cf. Reflexive space) and let be a semi-continuous monotone operator with the property of coerciveness:

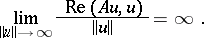Then for any 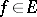the equation has at least one solution.

An operator 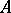defined on a set 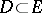with values in is called monotone on 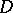if (1) holds for any 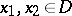, and it is called maximal monotone if it is monotone on and has no monotone proper (strict) extension.

Research into equations with monotone operators has been stimulated to a large extent by problems in the theory of quasi-linear elliptic and parabolic equations. For example, boundary value problems for quasi-linear parabolic equations lead to equations of the form

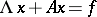(2)

in a suitable Banach space . The same equation also arises naturally in the investigation of the Cauchy problem for an abstract evolution equation with a non-linear operator in Banach spaces. If 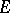is reflexive and 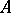is a bounded, semi-continuous and coercive operator with dense domain of definition in , then (2) is solvable for any 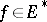. The idea of monotonicity has also been applied in the problem of almost-periodic solutions of non-linear parabolic equations.

References

[1]	F. Browder, "Non-linear parabolic boundary value problems of arbitrary order" Bull. Amer. Math. Soc. , 69 (1963) pp. 858–861
[2]	G.J. Minty, "On a "monotonicity" method for the solution of non-linear problems in Banach spaces" Proc. Nat. Acad. Sci. USA , 50 (1963) pp. 1038–1041
[3]	M.M. Vainberg, R.I. Kachurovskii, "On the variational theory of non-linear operators and equations" Dokl. Akad. Nauk SSSR , 129 : 6 (1959) pp. 1199–1202 (In Russian)
[4]	M.M. Vainberg, "Variational method and method of monotone operators in the theory of nonlinear equations" , Wiley (1973) (Translated from Russian)
[5]	J.-L. Lions, "Quelques méthodes de résolution des problèmes aux limites nonlineaires" , Dunod (1969)
[6]	B.M. Levitan, V.V. Zhikov, "Almost-periodic functions and differential equations" , Cambridge Univ. Press (1982) (Translated from Russian)
[7]	R.I. Kachurovskii, "Nonlinear monotone operators in Banach spaces" Russian Math. Surveys , 23 : 2 (1968) pp. 117–165 Uspekhi Mat. Nauk , 23 : 2 (1968) pp. 121–168