Gauss quadrature formula

The quadrature formula

in which the nodes (cf. Node) and the weights are so selected that the formula is exact for the functions

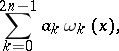where are given linearly independent functions (the integration limits may well be infinite). The formula was introduced by C.F. Gauss [1] for 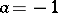, , . He obtained the following formula, which is exact for an arbitrary polynomial of degree not exceeding :

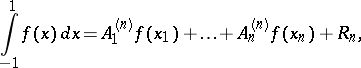where the 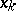are the roots of the Legendre polynomial (cf. Legendre polynomials) 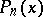, while and are defined by the formulas

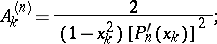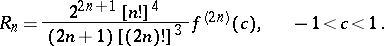The formula is used whenever the integrand is sufficiently smooth, and the gain in the number of nodes is substantial; for instance, if is determined from expensive experiments or during the computation of multiple integrals as repeated integrals. In such practical applications a suitable choice of the weight function and of the functions is very important.

Tables of nodes in Gauss' quadrature formula are available for wide classes of 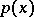and 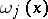[5]; in particular for 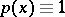, up to .

If , , 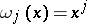Gauss' quadrature formula is employed in standard integration programs with an automatic step selection as a method of computing integrals by subdivision of subsegments [6].

References

[1]	C.F. Gauss, "Methodus nova integralium valores per approximationem inveniendi" , Werke , 3 , K. Gesellschaft Wissenschaft. Göttingen (1886) pp. 163–196
[2]	N.M. Krylov, "Approximate calculation of integrals" , Macmillan (1962) (Translated from Russian)
[3]	V.I. Krylov, L.T. Shul'gina, "Handbook on numerical integration" , Moscow (1966) (In Russian)
[4]	N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)
[5]	A.H. Stroud, "Gaussian quadrature formulas" , Prentice-Hall (1966)
[6]	, A standard program for the computation of single integrals of quadratures of Gauss' type : 26 , Moscow (1967) (In Russian)

Comments

A detailed investigation of the general Gauss formulas 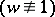was carried out by E.B. Christoffel [a3] and the quadrature coefficients are therefore also called Christoffel coefficients or Christoffel numbers (see also [a1]). Tables of these coefficients may be found in [a2].

References

[a1]	F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974)
[a2]	M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , 25 , Dover, reprint (1970)
[a3]	E.B. Christoffel, "Ueber die Gausssche Quadratur und eine Verallgemeinerung derselben" J. Reine Angew. Math. , 55 (1858) pp. 81–82
[a4]	P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1984)
[a5]	R. Piessens, et al., "Quadpack" , Springer (1983)