Continuous representation
From Encyclopedia of Mathematics
A linear representation 
of a topological group (semi-group, algebra) 
in a topological vector space 
such that the mapping 
of 
into 
defined by the formula 
, 
, 
, is continuous. If 
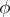is continuous in each argument separately, then in certain cases (for example, when 
is a locally compact group and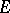 
is a Banach space) 
is automatically continuous jointly in the arguments, that is,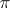 
is a continuous representation.
Comments
References
| [a1] | G. Warner, "Harmonic analysis on semi-simple Lie groups" , 1 , Springer (1972) |
How to Cite This Entry:
Continuous representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_representation&oldid=34030
Continuous representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_representation&oldid=34030
This article was adapted from an original article by A.I. Shtern (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article