Euclidean algorithm
A method for finding the greatest common divisor of two integers, two polynomials (and, in general, two elements of a Euclidean ring) or the common measure of two intervals. It was described in geometrical form in Euclid's Elements (3rd century B.C.).
For two positive integers 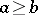 , the method is as follows. Division with remainder of
, the method is as follows. Division with remainder of  by
by 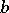 always leads to the result
always leads to the result 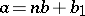 , where the quotient
, where the quotient  is a positive integer and the remainder
is a positive integer and the remainder 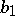 is either 0 or a positive integer less than
is either 0 or a positive integer less than 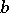 ,
, 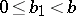 . Successive divisions are performed:
. Successive divisions are performed:
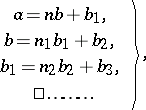 | (*) |
where the 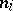 are positive integers and
are positive integers and 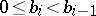 , until a remainder 0 is obtained. The series of equations (*) finishes thus:
, until a remainder 0 is obtained. The series of equations (*) finishes thus:
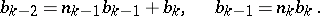 |
The least positive remainder 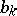 in this process is the greatest common divisor of
in this process is the greatest common divisor of  and
and 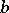 .
.
The Euclidean algorithms for polynomials or for intervals are similar to the one for integers. In the case of incommensurable intervals the Euclidean algorithm leads to an infinite process.
Comments
The Euclidean algorithm to determine the greatest common divisor of two integers 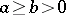 is quite fast. It can be shown that the number of steps required is at most
is quite fast. It can be shown that the number of steps required is at most
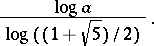 |
A slight extension of the algorithm also yields a solution of 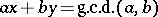 in
in  .
.
References
| [a1] | W.J. Leveque, "Topics in number theory" , 1 , Addison-Wesley (1956) pp. Chapt. 2 |
Euclidean algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euclidean_algorithm&oldid=33779