Limit cone
From Encyclopedia of Mathematics
of a convex surface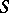 
The surface 
of the cone formed by the straight half-lines emanating from some point 
and belonging to the convex body bounded by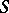 
. The limit cone is defined uniquely, up to a parallel displacement depending on the choice of 
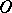. The notion of a limit cone is also defined for certain classes of non-convex surfaces, e.g. for so-called spherical one-sheet saddle surfaces.
References
| [1] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) |
Comments
References
| [a1] | R. Schneider, "Boundary structure and curvature of convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , Contributions to geometry , Birkhäuser (1979) pp. 13–59 |
| [a2] | H. Busemann, "Convex surfaces" , Interscience (1958) pp. Chapt. III, Sect. 15 |
How to Cite This Entry:
Limit cone. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit_cone&oldid=33769
Limit cone. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit_cone&oldid=33769
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article