Free associative algebra

The algebra 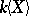of polynomials over a field in non-commuting variables in . The following universal property determines the algebra uniquely up to an isomorphism: There is a mapping such that any mapping from into an associative algebra 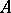with a unit over can be factored through in a unique way. The basic properties of are:

1) 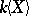can be imbedded in a skew-field (the Mal'tsev–Neumann theorem);

2) has a weak division algorithm, that is, the relation

where , all the 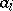are non-zero 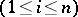, , always implies that there are an integer , , 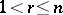and elements such that

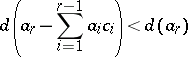and

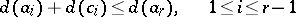(here is the usual degree of a polynomial , );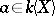

3) is a left (respectively, right) free ideal ring (that is, any left (respectively, right) ideal of is a free module of uniquely determined rank);

4) the centralizer of any non-scalar element of (that is, the set of elements that commute with a given element) is isomorphic to the algebra of polynomials over 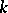in a single variable (Bergman's theorem).

References

[1]	P.M. Cohn, "Universal algebra" , Reidel (1981)
[2]	P.M. Cohn, "Free rings and their relations" , Acad. Press (1971)

'